Lecture
The resulting two-dimensional Fourier transform function 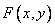 describing the image, the spectrum of this image is obtained, which is defined as
describing the image, the spectrum of this image is obtained, which is defined as
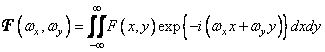 , (1.6.1)
, (1.6.1)
Where 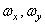 - spatial frequencies, and
- spatial frequencies, and 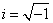 . If we denote the Fourier transform operator by
. If we denote the Fourier transform operator by 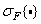 then you can write
then you can write
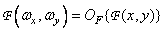 . (1.6.2)
. (1.6.2)
In general, the spectrum 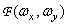 there is a complex value. It can be decomposed into real and imaginary parts:
there is a complex value. It can be decomposed into real and imaginary parts:
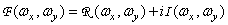 (1.6.3a)
(1.6.3a)
or present using amplitude and phase:
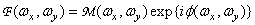 , (1.6.3b)
, (1.6.3b)
Where
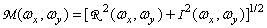 , (1.6.4a)
, (1.6.4a)
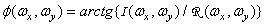 . (1.6.4b)
. (1.6.4b)
A sufficient condition for the existence of the Fourier spectrum of a function 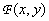 is the absolute integrability of this function, i.e. condition
is the absolute integrability of this function, i.e. condition
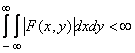 . (1.6.5)
. (1.6.5)
Source function 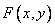 can be restored by the inverse Fourier transform:
can be restored by the inverse Fourier transform:
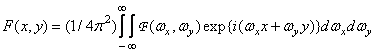 . (1.6.6a)
. (1.6.6a)
This ratio in the operator form can be written as
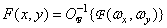 . (1.6.6b)
. (1.6.6b)
Since the core of the two-dimensional Fourier transform is separable, this transformation can be performed in two stages. First located
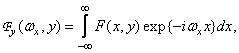 (1.6.7)
(1.6.7)
and then
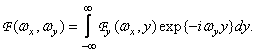 (1.6.8)
(1.6.8)
Below are some useful properties of the two-dimensional Fourier transform. Their evidence can be found in books [1, 2].
Functional properties
If the function 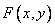 separable by spatial variables so that
separable by spatial variables so that
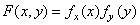 , (1.6.9)
, (1.6.9)
that
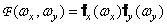 , (1.6.10)
, (1.6.10)
Where  - one-dimensional Fourier spectra of functions
- one-dimensional Fourier spectra of functions 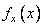 ,
, 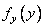 . If a
. If a 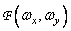 there is a Fourier spectrum of the function
there is a Fourier spectrum of the function 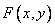 then
then 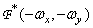 is the Fourier spectrum of the function
is the Fourier spectrum of the function 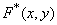 . (An asterisk denotes complex conjugation.) If the function
. (An asterisk denotes complex conjugation.) If the function 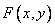 symmetric, i.e.
symmetric, i.e. 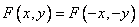 then
then 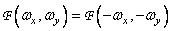 .
.
Linearity
The Fourier transform operator is linear:
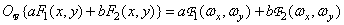 , (1.6.11)
, (1.6.11)
Where 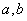 - permanent.
- permanent.
Zoom
A change in the spatial scale leads to an inverse change in the scale of spatial frequencies and a proportional change in the values of the spectrum:
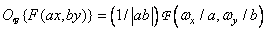 . (1.6.12)
. (1.6.12)
Therefore, the compression along one of the axes of the plane  leads to stretching along the corresponding axis of the frequency plane and vice versa. There is also a proportional change in the values of the spectrum.
leads to stretching along the corresponding axis of the frequency plane and vice versa. There is also a proportional change in the values of the spectrum.
Shift
The shift (change of coordinates) on the initial plane leads to phase changes on the frequency plane:
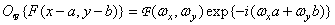 (1.6.13a)
(1.6.13a)
On the contrary, a shift in the frequency plane causes phase changes of the original function:
 (1.6.13b)
(1.6.13b)
Convolution
The Fourier spectrum of a function obtained by convolving two functions is equal to the product of the spectra of the original functions:
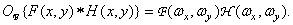 (1.6.14)
(1.6.14)
The converse theorem states that
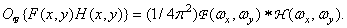 (1.6.15)
(1.6.15)
Parseval's theorem
Two representations of the image energy - through the function 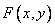 and Fourier spectrum
and Fourier spectrum 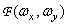 - are related as follows:
- are related as follows:
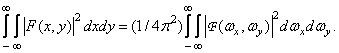 (1.6.16)
(1.6.16)
Spectrum theorem for the autocorrelation function
The Fourier spectrum of the two-dimensional autocorrelation function of the image is equal to the square of the Fourier spectrum module of this image:
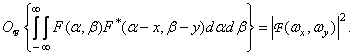 (1.6.17)
(1.6.17)
Spectra of spatial derivatives
Fourier spectra of the first spatial derivatives of the function 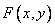 associated with its Fourier spectrum by the following relations:
associated with its Fourier spectrum by the following relations:
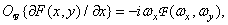 (1.6.18a)
(1.6.18a)
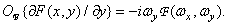 (1.6.18b)
(1.6.18b)
Therefore, the spectrum of the Laplacian is
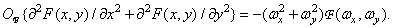 (1.6.19)
(1.6.19)
Comments
To leave a comment
Digital image processing
Terms: Digital image processing