Lecture
When using the cyclic superposition operator, the arrays of the input and output images, as well as the impulse response, must be periodic in spatial variables with the same period. For the sake of unity, we assume, as before, that all these arrays have finite dimensions. Assume also that the array of source samples 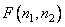 by size
by size 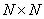 placed in the upper left corner of the array containing
placed in the upper left corner of the array containing 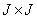 zeros
zeros 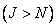 i.e. an extended array is formed
i.e. an extended array is formed
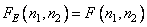 at
at 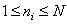 , (9.3.1а)
, (9.3.1а)
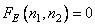 at
at 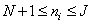 . (9.3.1b)
. (9.3.1b)
Similarly, an extended array of impulse response samples is formed:
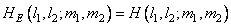 at
at 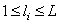 , (9.3.2а)
, (9.3.2а)
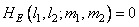 at
at 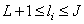 . (9.3.2b)
. (9.3.2b)
Next, we form periodically continued arrays 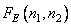 and
and 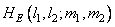 , repeating (propagating) extended arrays with a period of
, repeating (propagating) extended arrays with a period of 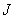 counts. The cyclic convolution of these arrays is by definition equal to
counts. The cyclic convolution of these arrays is by definition equal to
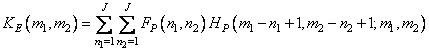 . (9.3.3)
. (9.3.3)
The similarity of this expression with equality (9.1.1), describing the superposition of finite arrays, is striking. In fact, if 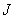 chosen so that
chosen so that  then
then 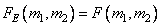 at
at 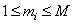 . It should also be noted the similarity of cyclic superposition with the superposition of discretized arrays. These relationships become clearer when using the vector representation of cyclic superposition.
. It should also be noted the similarity of cyclic superposition with the superposition of discretized arrays. These relationships become clearer when using the vector representation of cyclic superposition.
Assume that arrays 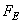 and
and 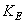 presented accordingly
presented accordingly 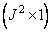 -component vectors
-component vectors 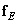 and
and 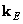 . Then for the operation of cyclic superposition, you can write the ratio
. Then for the operation of cyclic superposition, you can write the ratio
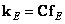 , (9.3.4)
, (9.3.4)
Where 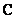 - matrix of array elements
- matrix of array elements 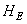 size
size  . The cyclic superposition operator can be conveniently expressed as a block matrix with blocks
. The cyclic superposition operator can be conveniently expressed as a block matrix with blocks 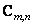 size
size 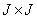 :
:
 , (9.3.5)
, (9.3.5)
Where
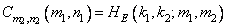 , (9.3.6)
, (9.3.6)
and 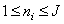 and
and 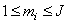 a
a 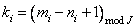 and
and 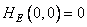 . It should be noted that each row and each column of the block matrix
. It should be noted that each row and each column of the block matrix 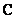 contain
contain 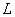 nonzero blocks. If the array of impulse response samples is spatially invariant, then
nonzero blocks. If the array of impulse response samples is spatially invariant, then
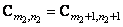 (9.3.7)
(9.3.7)
and any row (or column) can be obtained by cyclically rearranging the blocks of the first row (or the first column). In fig. 9.3.1, and the example of the cyclic convolution operator is given, when the input and output arrays have dimensions 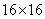
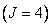 , and the size of the array of samples of the impulse response is equal to
, and the size of the array of samples of the impulse response is equal to 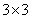
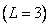 . In fig. 9.3.1, b shows the matrix structure of the same operator with
. In fig. 9.3.1, b shows the matrix structure of the same operator with 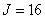 and
and 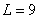 when the impulse response is Gaussian.
when the impulse response is Gaussian.

Fig. 9.3.1. Examples of matrices of the cyclic convolution operator.
a - the general case 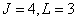 ; b - impulse response of the Gaussian form,
; b - impulse response of the Gaussian form, 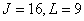 .
.
If the impulse response is spatially invariant and separable, then
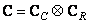 , (9.3.8)
, (9.3.8)
Where 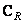 and
and 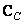 - view matrix
- view matrix
 , (9.3.9)
, (9.3.9)
which size is equal 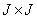 . In this case, the two-dimensional cyclic convolution is calculated in accordance with the ratio
. In this case, the two-dimensional cyclic convolution is calculated in accordance with the ratio
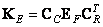 . (9.3.10)
. (9.3.10)
Comments
To leave a comment
Digital image processing
Terms: Digital image processing