8.2. STATISTICAL DESCRIPTION OF IMAGES UNDER LINEAR TRANSFORMATION

If the array of samples of the input image is a realization of a random process with known first and second moments, then for a given linear transformation you can find the first and second moments for the array of samples of the output image. The average value of the output array is

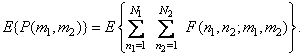(8.2.1a)

However, the averaging operator is linear, and therefore

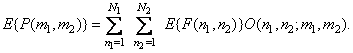(8.2.1b)

The correlation function of the array of samples of the output image is

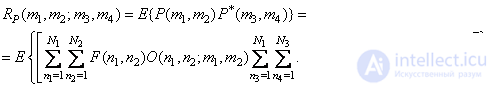(8.2.2a)

After multiplying the series and calculating the average, we get the expression

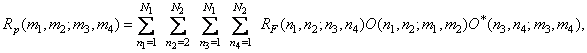(8.2.2b)

Where 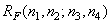- the correlation function of the array of samples of the original image. The covariance function of the processed image is determined similarly.

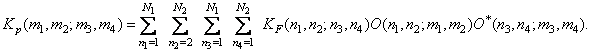(8.2.3)

If the arrays of samples of the input and output images are presented in vector form, then the expressions for their moments can be written more compactly. The average value of the output vector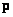

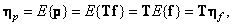(8.2.4)

and its correlation matrix

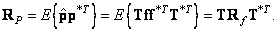(8.2.5)

Vector Covariance Matrix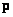

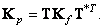(8.2.6)

The application of these theoretical principles to the operators of superposition and unitary transformation is described in subsequent chapters.