8.6. APPROXIMATE SOLUTIONS OF INCOMPATIBLE SYSTEMS OF LINEAR EQUATIONS

Incompatibility of the system of equations 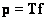means that for none of the possible assessments 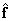the system will not go over into identity with the substitution 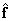instead 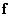. In such cases, the system of equations can be converted to

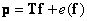(8.6.1)

Where 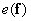- error vector depending on 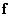. We now find the value of the estimate. 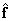at which the value of the error is minimal, expressed by two equivalent ratios:

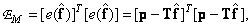(8.6.2а)

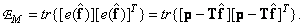(8.6.2b)

Let the symbol 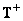denotes a pseudoinverse matrix, which is used to estimate

(8.6.3)

Adding and removing work 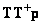inside both brackets of the relation (8.6.2а), we get

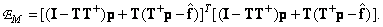(8.6.4)

After multiplying we have

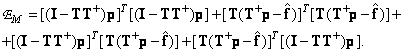(8.6.5)

Two cross terms will be zero if 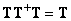and 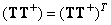. However, under these conditions, the matrix 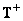is the least squares inversion matrix, i.e. 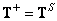. Then the error will be equal to the sum of two positive terms:

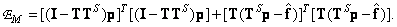(8.6.6)

The second term of equality (8.6.6) turns into zero, since 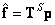. Therefore, the error is reduced to

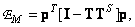(8.6.7а)

or, which is the same,

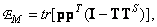(8.6.7b)

As expected, the error is zero if .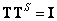

The solution obtained by least-squares pseudo-inversion may not be the only one. If at pseudo-reversal to enter additional conditions 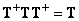and 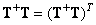for which the matrix 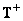is a generalized inverse (i.e. 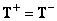), it can be shown that the estimate obtained using this matrix ( 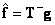), is a solution with a minimum rate in the sense that

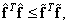(8.6.8)

Where 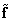- arbitrary estimate, found by the method of least squares. If the generalized inverse matrix 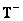has rank 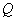and satisfies the definition (8.3.5), then the product 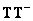not necessarily equal to the identity matrix, but the error can be found from relations (8.6.7). If the matrix 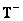has rank 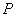, i.e. corresponds to the definition (8.3.6), then 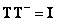the error is zero.

The following chapters will show how these theoretical assumptions are applied to correct, analyze, and encode images.