Lecture
The singular transformation [34] is a two-dimensional unitary transformation based on the singular decomposition of matrices (see Chapter 5). A direct singular transformation is by definition equal to
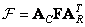 , (10.9.1)
, (10.9.1)
and the inverse transform
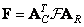 . (10.9.2)
. (10.9.2)
String Conversion Matrix 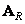 provides a diagonalization operation
provides a diagonalization operation
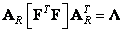 , (10.9.3)
, (10.9.3)
Where 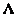 - diagonal matrix, elements
- diagonal matrix, elements 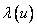 which are eigenvalues of the matrix
which are eigenvalues of the matrix 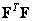 . Similarly
. Similarly
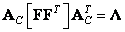 . (10.9.4)
. (10.9.4)
Substituting expression (10.9.2) into equalities (10.9.3) and (10.9.4), we get
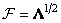 , (10.9.5)
, (10.9.5)
where elements of the diagonal matrix  are numbers
are numbers 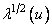 called the singular values of the matrix
called the singular values of the matrix 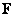 and equal to the square root of the corresponding eigenvalues
and equal to the square root of the corresponding eigenvalues 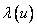 .
.
The image matrix can be written in a very compact form using the matrix product of vectors obtained by singular decomposition. According to equality (10.1.14b),
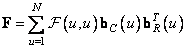 , (10.9.6)
, (10.9.6)
Where 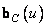 and
and 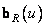 are vectors consisting of elements
are vectors consisting of elements 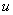 columns of matrices
columns of matrices 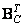 and
and 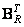 .
.
Using a singular transformation, the image matrix 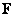 containing
containing 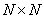 items can be fully described
items can be fully described 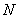 values representing
values representing 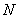 coefficients
coefficients 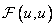 . However, it should be noted that the specific values of the elements of the transformation matrices in rows and columns in this case depend on the image elements.
. However, it should be noted that the specific values of the elements of the transformation matrices in rows and columns in this case depend on the image elements.
In fig. 10.9.1 shows an example of a singular transformation of the image. Shown here are works 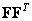 and
and 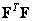 as well as the corresponding transformation matrices in rows
as well as the corresponding transformation matrices in rows 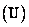 and by columns
and by columns 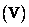 . The singular values of the image in question are shown in Fig. 10.9.2. In fig. 10.9.3 shows several matrix products
. The singular values of the image in question are shown in Fig. 10.9.2. In fig. 10.9.3 shows several matrix products 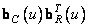 .
.

Fig. 10.9.1. Singular transformation of the image "Portrait". All arrays from 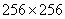 elements are derived from size arrays
elements are derived from size arrays 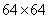 element by means of bilinear interpolation.
element by means of bilinear interpolation.
and - the initial image, a matrix 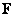 ; b - the result of a singular transformation matrix
; b - the result of a singular transformation matrix 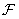 ; in - matrix
; in - matrix 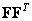 ; g - matrix
; g - matrix 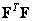 ; d - the matrix consisting of the modules of the elements of the matrix
; d - the matrix consisting of the modules of the elements of the matrix 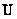 ; е - the matrix consisting of the modules of the elements of the matrix
; е - the matrix consisting of the modules of the elements of the matrix 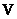 .
.
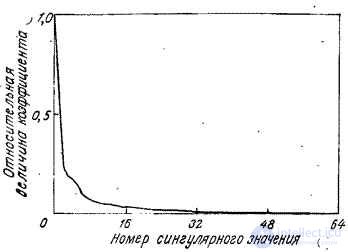
Fig. 10.9.2. Singular values of the image "Portrait".

Fig. 10.9.3. Basic images for the image "Portrait".
Figures a, b, c, d, d, e correspond 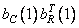 ,
, 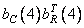 ,
, 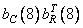 ,
, 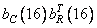 ,
, 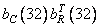 ,
, 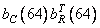 .
.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing