Lecture
As already noted, for the convolution operator of finite arrays or the discretized convolution operator, the equivalent output vector can be found by choosing certain elements of the extended output cyclic convolution vector 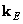 or its corresponding matrix
or its corresponding matrix 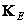 . This situation in combination with equality (11.2.13) leads to a very efficient procedure for calculating convolution, consisting of the following steps:
. This situation in combination with equality (11.2.13) leads to a very efficient procedure for calculating convolution, consisting of the following steps:
1. Write the impulse response matrix in the upper left corner of the zero matrix. 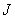 th order, and
th order, and 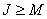 for the case of convolution of finite arrays and
for the case of convolution of finite arrays and 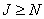 for discretized convolution. Perform a two-dimensional Fourier transform of the extended impulse response matrix.
for discretized convolution. Perform a two-dimensional Fourier transform of the extended impulse response matrix.
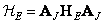 . (11.3.1)
. (11.3.1)
2. Write the matrix of the original image in the upper left corner of the zero matrix 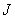 -th order and perform a two-dimensional Fourier transform of the augmented matrix of the original image
-th order and perform a two-dimensional Fourier transform of the augmented matrix of the original image
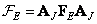 . (11.3.2)
. (11.3.2)
3. Perform scalar multiplication
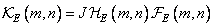 , (11.3.3)
, (11.3.3)
Where 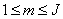 and
and 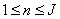 .
.
4. Perform inverse Fourier transform
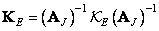 . (11.3.4)
. (11.3.4)
5. After selecting the desired elements to form the desired output matrix
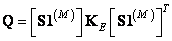 (11.3.5a)
(11.3.5a)
or
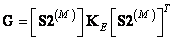 . (11.3.5b)
. (11.3.5b)
It is important that order  extended matrices
extended matrices  and
and 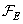 satisfied the corresponding inequalities. With
satisfied the corresponding inequalities. With 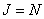 on the left and top edges of the output matrix there will be bands of erroneous elements having a width of
on the left and top edges of the output matrix there will be bands of erroneous elements having a width of 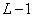 the countdown (fig. 11.3.1, a, b). They are formed as a result of the so-called cyclic error associated with the incorrect application of the FFT method to calculate convolution. In addition, when performing convolution of finite arrays (
the countdown (fig. 11.3.1, a, b). They are formed as a result of the so-called cyclic error associated with the incorrect application of the FFT method to calculate convolution. In addition, when performing convolution of finite arrays ( 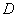 -convolution) will be lost elements of the output array, arranged by stripes in the right and lower parts of it. If we put
-convolution) will be lost elements of the output array, arranged by stripes in the right and lower parts of it. If we put 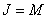 then at
then at 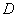 - The output matrix will be completely filled with the correct readings. To calculate
- The output matrix will be completely filled with the correct readings. To calculate 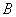 -convolution with
-convolution with 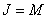 , it is necessary to cut off the right and bottom edges of the original matrix. However, the result is that the elements of the output array, located on the top and on the left, will be erroneous.
, it is necessary to cut off the right and bottom edges of the original matrix. However, the result is that the elements of the output array, located on the top and on the left, will be erroneous.
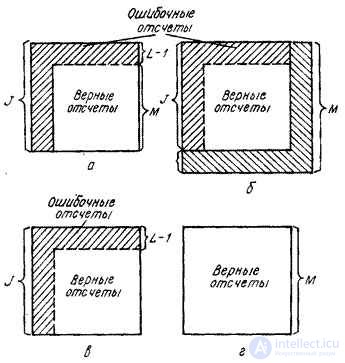
Fig. 11.3.1. Cyclic errors. (Bottom and right sides of the matrix 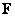 cut off.)
cut off.)
a - type filtering 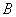 ;
; 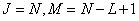 .
.
b - type filtering 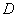 ;
; 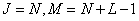 .
.
c - type filtering 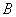 ;
; 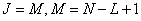 .
.
g - type filtering 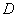 ;
; 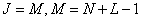 .
.
In signal processing, in many cases, it turns out that different input arrays are affected by operators with the same impulse response and, consequently, the first stage of the algorithm (calculation 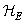 ) enough to run only once. When using the FFT algorithm for the cases of direct and inverse transformations, it is required to perform approximately
) enough to run only once. When using the FFT algorithm for the cases of direct and inverse transformations, it is required to perform approximately 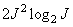 arithmetic operations. Scalar multiplication is done for
arithmetic operations. Scalar multiplication is done for 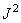 operations, i.e., everything is required
operations, i.e., everything is required 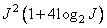 operations. If the input matrix contains
operations. If the input matrix contains 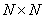 items, output
items, output 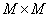 and impulse response matrix
and impulse response matrix 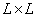 elements, then to calculate the final convolution is required
elements, then to calculate the final convolution is required 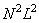 operations, and for discretized convolution
operations, and for discretized convolution 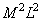 operations. If size
operations. If size 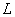 impulse response matrices are large enough compared to the size
impulse response matrices are large enough compared to the size 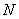 the original matrix, the convolution with the transformation turns out to be more efficient than the direct convolution, and the number of operations can be reduced ten times or more. In fig. 11.3.2 shows the graph of dependence
the original matrix, the convolution with the transformation turns out to be more efficient than the direct convolution, and the number of operations can be reduced ten times or more. In fig. 11.3.2 shows the graph of dependence 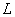 from
from 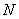 for the case when both methods for calculating the convolution of finite arrays (direct and with Fourier transform) have the same efficiency. The jaggedness of the graphics is due to the fact that with increasing
for the case when both methods for calculating the convolution of finite arrays (direct and with Fourier transform) have the same efficiency. The jaggedness of the graphics is due to the fact that with increasing 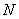 parameter
parameter 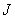 changes in steps, taking values 64, 128, 256, etc.
changes in steps, taking values 64, 128, 256, etc.
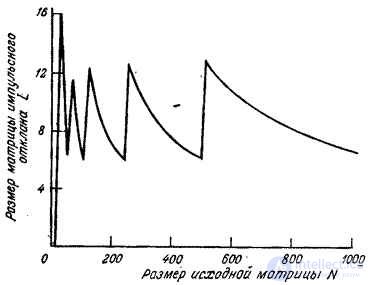
Fig. 11.3.2. Comparison of the effectiveness of two methods of obtaining the final convolution: direct and with the Fourier transform.
The calculation of the convolution with the Fourier transform requires a smaller number of operations than in the case of its direct calculation, if the length of the impulse response is large enough. However, if the processed image is also large, the relative efficiency of the method using the Fourier transform decreases. In addition, when calculating the Fourier transform of large matrices, difficulties arise in ensuring the accuracy of the calculations. Both problems can be resolved by resorting to block-based image filtering, when a large matrix is subdivided into a series of overlapping blocks processed alternately [2, 7–9].
In fig. 11.3.3, and it is shown how the block containing the 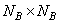 items. After convolving it with an impulse response consisting of
items. After convolving it with an impulse response consisting of 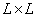 elements, it turns out a block of size
elements, it turns out a block of size 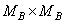 elements, which are placed in the upper left corner of the output matrix (Fig. 11.3.3, a). Next, from the processed matrix extract the next block size
elements, which are placed in the upper left corner of the output matrix (Fig. 11.3.3, a). Next, from the processed matrix extract the next block size 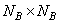 elements and from it receive the second block of the processed size image
elements and from it receive the second block of the processed size image 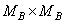 adjacent to the first. As shown in fig. 11.3.3, b, the second block of the original image must overlap with the first block in the strip width
adjacent to the first. As shown in fig. 11.3.3, b, the second block of the original image must overlap with the first block in the strip width 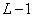 element. Then the processed blocks will dock without a gap. This process continues until all blocks adjacent to the top row of the matrix are processed. If the last block in this block line is incomplete, add zero elements to it. Next, remove the block located at the beginning of the second row and overlapping with the blocks of the first row in the strip width
element. Then the processed blocks will dock without a gap. This process continues until all blocks adjacent to the top row of the matrix are processed. If the last block in this block line is incomplete, add zero elements to it. Next, remove the block located at the beginning of the second row and overlapping with the blocks of the first row in the strip width 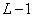 element. The process continues until all elements of the processed image have been determined.
element. The process continues until all elements of the processed image have been determined.
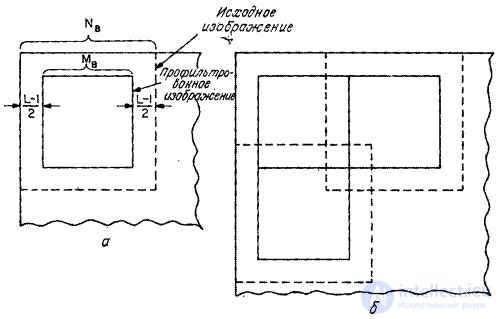
Fig. 11.3.3. Placing blocks with block image filtering.
a - the first block; b - the second blocks in the row and column of blocks.
To obtain convolution with the Fourier transform is required
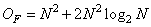 (11.3.6)
(11.3.6)
operations. When block processing, when the block size is  necessary
necessary
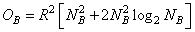 (11.3.7)
(11.3.7)
operations where the number of blocks 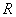 - fraction value rounded up
- fraction value rounded up 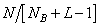 . Hunt [9] determined how the optimal block size depends on the size of the matrices of the original image and the impulse response.
. Hunt [9] determined how the optimal block size depends on the size of the matrices of the original image and the impulse response.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing