Lecture
Any analog value to be processed in a digital computer or digital system must be represented as an integer number proportional to the value of this value. The process of converting samples with a continuous set of values into samples with discrete values is called quantization. The next two sections give a mathematical analysis of the quantization process, which is valid not only for images, but in general for a wide class of signals that one has to face in image processing systems. Then the processing of quantized samples is considered. The last two sections describe the subjective effects that occur when quantizing single-color and color images.
Fig. 6.1.1 illustrates a typical example of scalar quantization. In the quantization process, the sample value of the analog signal is compared with a set of threshold levels. If the sample falls in the interval between two adjacent threshold levels, then the value of the fixed quantization level corresponding to the given interval is attributed to it. In a digital system, a binary code combination is assigned to each quantized sample. In this example, a uniform code is applied having a constant length of code combinations.
Starting a quantitative analysis of quantization of scalar quantities, we assume that 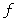 and
and 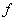 denote, respectively, the values of the reference of the actual scalar signal before and after quantization. It is assumed that
denote, respectively, the values of the reference of the actual scalar signal before and after quantization. It is assumed that 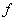 - random variable with probability density
- random variable with probability density 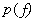 . In addition, it is assumed that
. In addition, it is assumed that 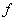 does not go beyond a certain interval:
does not go beyond a certain interval:
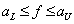 , (6.1.1)
, (6.1.1)
Where 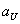 and
and 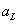 - upper and lower limits of the interval.
- upper and lower limits of the interval.
When solving the quantization problem, it is necessary to choose such a set of threshold levels. 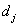 and quantization levels
and quantization levels 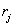 , what if
, what if
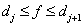 , (6.1.2)
, (6.1.2)
then the original count is replaced by a number equal to the quantization level 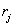 . In fig. 6.1.2, and an example is given of the arrangement of threshold levels and quantization levels on a segment of the numerical axis containing
. In fig. 6.1.2, and an example is given of the arrangement of threshold levels and quantization levels on a segment of the numerical axis containing  threshold levels. Another common form of representing the characteristics of a quantizer is a step curve (Fig. 6.1.2, b).
threshold levels. Another common form of representing the characteristics of a quantizer is a step curve (Fig. 6.1.2, b).
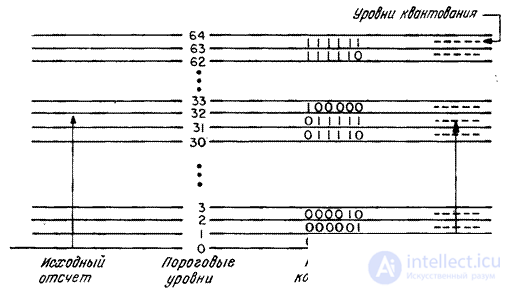
Fig. 6.1.1. An example of signal quantization.
The quantization levels and threshold levels are chosen so as to minimize to a minimum some given value characterizing the quantization error, i.e. the degree of difference between 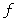 and
and 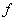 . As a measure of quantization error, a rms error is usually chosen. If a
. As a measure of quantization error, a rms error is usually chosen. If a 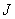 - the number of quantization levels, then the root-mean-square quantization error is
- the number of quantization levels, then the root-mean-square quantization error is
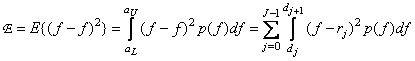 . (6.1.3)
. (6.1.3)
If the number 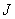 large, then the probability density of the values of the quantized signal at each of the intervals
large, then the probability density of the values of the quantized signal at each of the intervals 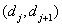 can be considered constant and equal
can be considered constant and equal 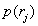 . Consequently,
. Consequently,
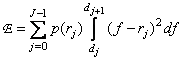 (6.1.4)
(6.1.4)
or after calculating the integrals
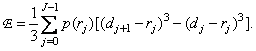 (6.1.5)
(6.1.5)
Optimal quantization level position 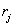 in the interval
in the interval 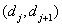 can be found by solving the problem of the minimum error
can be found by solving the problem of the minimum error 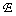 as functions
as functions 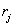 . Equating zero derivative
. Equating zero derivative
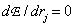 , (6.1.6)
, (6.1.6)
we get
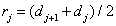 . (6.1.7)
. (6.1.7)
Thus, under the assumptions made, the optimal position of the quantization level is the midpoint of the interval between adjacent threshold levels.
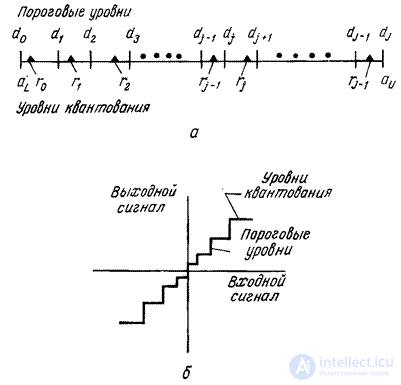
Fig. 6.1.2. Thresholds and quantization levels.
Substituting the corresponding values in the expression for the quantization error, we get
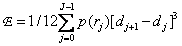 . (6.1.8)
. (6.1.8)
The optimal position of the threshold levels can be determined by finding the minimum error 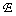 Lagrange multipliers. Using this method, Panther and Data [1] showed that the positions of threshold levels are fairly accurately determined by the formula
Lagrange multipliers. Using this method, Panther and Data [1] showed that the positions of threshold levels are fairly accurately determined by the formula
 (6.1.9a)
(6.1.9a)
Where
 , (6.1.9b)
, (6.1.9b)
but 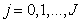 . If the probability density of sample values is uniform, then the threshold levels will be spaced evenly. With non-uniform densities, threshold levels are more common in those areas where the probability density is high, and less often where it is low. For most types of probability density, which are usually used in image description, integrals (6.1.9) cannot be taken, and the position of threshold levels has to be found using numerical integration.
. If the probability density of sample values is uniform, then the threshold levels will be spaced evenly. With non-uniform densities, threshold levels are more common in those areas where the probability density is high, and less often where it is low. For most types of probability density, which are usually used in image description, integrals (6.1.9) cannot be taken, and the position of threshold levels has to be found using numerical integration.
If the number of quantization levels is small, then the approximation by which equality (6.1.4) is obtained becomes unjustified and the exact expression for the error (6.1.3) should be used. Differentiating it by variables 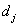 and
and 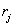 and equating the derivatives to zero, we get
and equating the derivatives to zero, we get
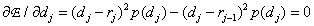 (6.1.10a)
(6.1.10a)
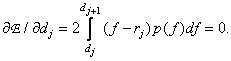 (6.1.10b)
(6.1.10b)
After transformations we come to the system of equations
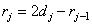 (6.1.11a)
(6.1.11a)
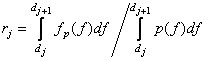 . (6.1.11b)
. (6.1.11b)
Solving these equations in a recurrent way, it is possible for a given probability density 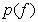 find the optimal values of threshold levels and quantization levels. Max [2] solved this problem for Gaussian density and compiled tables of optimal placement of threshold levels depending on the number of quantization levels. In tab. 6.1.1 shows the location of the quantization levels and threshold levels in the Max quantizer for the densities of the Gauss, Laplace, Rayleigh, and uniform probability distributions.
find the optimal values of threshold levels and quantization levels. Max [2] solved this problem for Gaussian density and compiled tables of optimal placement of threshold levels depending on the number of quantization levels. In tab. 6.1.1 shows the location of the quantization levels and threshold levels in the Max quantizer for the densities of the Gauss, Laplace, Rayleigh, and uniform probability distributions.
Table 6.1.1. The location of the quantization levels and threshold levels in the Max quantizer
|
Number of charges |
Uniform |
Gauss |
Laplace |
Rayleigh |
||||
|
one |
-1,0000 |
-0,5000 |
-0.7979 |
-0.7071 |
0,0000 |
1.2657 |
||
|
|
0,0000 |
0.5000 |
0,0000 |
0.7979 |
0,0000 |
0.7071 |
2.0985 |
2.9313 |
|
|
1.0000 |
|
|
|
|
|||
|
2 |
-1,0000 |
-0.7500 |
-1,5104 |
-1,8340 |
0,0000 |
0,8079 |
||
|
|
-0,5000 |
-0,2500 |
-0.9816 |
-0.4528 |
-1.1269 |
-0,4198 |
1.2545 |
1.7010 |
|
|
-0.0000 |
0,2500 |
0,0000 |
0.4528 |
0,0000 |
0.4198 |
2.1667 |
2.6325 |
|
|
0.5000 |
0.7500 |
0.9816 |
1.5104 |
1.1269 |
1.8340 |
3.2465 |
3,8604 |
|
|
1.0000 |
|
|
|
|
|||
|
3 |
-1,0000 |
-0,8750 |
-2.1519 |
-3.0867 |
0,0000 |
0.5016 |
||
|
|
-0.7500 |
-0,6250 |
-1,7479 |
-1,3439 |
-2.3796 |
-1,6725 |
0.7619 |
1,0222 |
|
|
-0,5000 |
-0.3750 |
-1.0500 |
-0.7560 |
-1,2527 |
-0.8330 |
1.2594 |
1.4966 |
|
|
-0,2500 |
-0.1250 |
-0,5005 |
-0,2451 |
-0,5332 |
-0,2334 |
1.7327 |
1.9688 |
|
|
0,0000 |
0.1250 |
0,0000 |
0.2451 |
0,0000 |
0.2334 |
2.2182 |
2.4675 |
|
|
0,2500 |
0.3750 |
0.5005 |
0.7560 |
0.5332 |
0.8330 |
2.7476 |
3.0277 |
|
|
0.5000 |
0.6250 |
1,0500 |
1.3439 |
1.2527 |
1.6725 |
3.3707 |
3.7137 |
|
|
0.7500 |
0.8750 |
1.7479. |
2.1519 |
2.3796 |
3.0867 |
4.2124 |
4.7111 |
|
|
1.0000 |
|
|
|
|
|||
|
four |
-1,0000 |
-0.9375 |
-2,7326 |
-4,4311 |
0,0000 |
0.3057 |
||
|
|
-0,8750 |
-0.8125 |
-2,4008 |
-2.0690 |
-3.7240 |
-3,0169 |
0.4606 |
0.6156 |
|
|
-0.7500 |
-0,6875 |
-1,8435 |
-1.6180 |
-2.5971 |
-2,1773 |
0.7509 |
0.8863 |
|
|
-0,6250 |
-0,5625 |
-1.4371 |
-1.2562 |
-1,8776 |
-1,5778 |
1,0130 |
1,1397 |
|
|
-0,5000 |
-0.4375 |
-1,0993 |
-0.9423 |
-1,3444 |
-1.1110 |
1.2624 |
1.3850 |
|
|
-0.3750 |
-0.3125 |
-0.7995 |
-0.6568 |
-0,9198 |
-0.7287 |
1.5064 |
1.6277 |
|
|
-0,2500 |
-0.1875 |
-0,5224 |
-0.3880 |
-0,5667 |
-0.4048 |
1.7499 |
1.8721 |
|
|
-0.1250 |
-0.0625 |
-0.2582 |
-0,1284 |
-0,2664 |
-0.1240 |
1.9970 |
2.1220 |
|
|
0,0000 |
0.0625 |
0,0000 |
0.12284 |
0,0000 |
0.1240 |
2.2517 |
2.3814 |
|
|
0.1250 |
0.1875 |
0.2582 |
0.3880 |
0.2644 |
0.4048 |
2.5182 |
2.6550 |
|
|
0,2500 |
0.3125 |
0.5224 |
0.6568 |
0.5667 |
0.7287 |
2.8021 |
2,9492 |
|
|
0.3750 |
0.4375 |
0.7995 |
0.9423 |
0.9198 |
1.1110 |
3.1110 |
3.2729 |
|
|
0.5000 |
0.5625 |
1,0993 |
3.2562 |
1.3444 |
1.5778 |
3.4566 |
3.6403 |
|
|
0.6250 |
0.6875 |
1.4371 |
1.6180 |
1.8776 |
2.1773 |
3.8588 |
4.0772 |
|
|
0.7500 |
0.8125 |
1.8435 |
2.0690 |
2.5971 |
3,0169 |
4.3579 |
4.6385 |
|
|
0.8750 |
0.9375 |
2.4008 |
2,7326 |
3.7240 |
4.4311 |
5.0649 |
5.4913 |
|
|
1.0000 |
|
|
|
|
|||
It is easy to show that if the threshold levels and quantization levels are chosen according to equality (6.1.11), then the root-mean-square quantization error decreases to
 (6.1.12a)
(6.1.12a)
or in shorter form
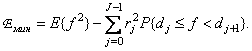 (6.1.12b)
(6.1.12b)
For the particular case of the density of the uniform probability distribution, the minimum root mean square error is equal to
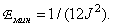 (6.1.13)
(6.1.13)
For most other types of probability density, quantization error has to be determined by calculations.
Uneven quantization can be reduced to a uniform using a nonlinear transformation, as shown in Fig. 6.1.3. The counting is subjected to nonlinear transformation, will be evenly quantized and subjected to the inverse nonlinear transformation [3]. In quantization systems with transformation, they strive to make the probability density of the transformed samples at the input of the quantizer uniform. The converted count (Fig. 6.1.3) is
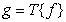 , (6.1.14)
, (6.1.14)
moreover, nonlinear transformation 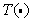 chosen such that the probability density
chosen such that the probability density 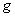 turns out to be uniform, i.e.
turns out to be uniform, i.e.
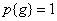 . (6.1.15)
. (6.1.15)
in the interval 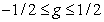 . If a
. If a 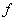 - a random value with zero mean, then the desired characteristic of the nonlinear element has the form [4]
- a random value with zero mean, then the desired characteristic of the nonlinear element has the form [4]
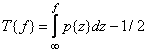 . (6.1.16)
. (6.1.16)

Fig. 6.1.3. Quantizer with compression.
Table 6.1.2. Transformation quantization
|
Probability density |
Direct conversion |
Inverse transform |
|
Gaussian Rayleigh Laplace
|
|
|
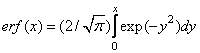 |
||
Thus, it coincides with the probability distribution function of a quantity. In tab. 6.1.2 shows the characteristics of direct and inverse nonlinear transformations for the densities of the probability distributions of Gauss, Rayleigh, Laplace.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing