Lecture
Usually, quantization of a set of samples is performed sequentially. Each sample is treated as a scalar and quantized independently of the other samples using the methods described in the previous section. However, it is often possible to reduce the quantization error if all samples are quantized together.
Consider the signal 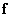 representing the size vector
representing the size vector 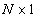 . We assume that this vector is an implementation of a random vector with
. We assume that this vector is an implementation of a random vector with 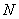 -dimensional probability density
-dimensional probability density
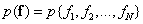 . (6.2.1)
. (6.2.1)
When quantizing a vector 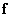
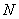 -dimensional vector space is divided into
-dimensional vector space is divided into 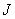 quantization cells
quantization cells 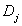 each of which corresponds to one of
each of which corresponds to one of 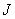 quantized vectors. Vector signal
quantized vectors. Vector signal 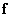 replaced by a quantized vector
replaced by a quantized vector 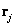 if a
if a 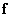 falls into the cell
falls into the cell 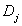 . In fig. 6.2.1 shows examples of vector quantization in one-, two-, and three-dimensional spaces. In a similar general formulation of the vector quantization problem, the vector signal
. In fig. 6.2.1 shows examples of vector quantization in one-, two-, and three-dimensional spaces. In a similar general formulation of the vector quantization problem, the vector signal 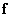 converted to vector
converted to vector 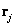 but vector components
but vector components 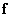 however, they will not necessarily be quantized separately over a set of discrete threshold levels.
however, they will not necessarily be quantized separately over a set of discrete threshold levels.
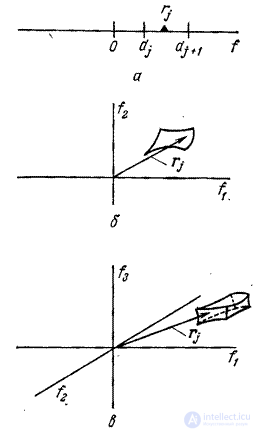
Fig. 6.2.1. Quantization cells in vector space: a - one-dimensional space; b - two-dimensional space; in - three-dimensional space.
The rms error of vector quantization can be represented as a sum
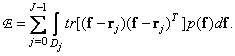 (6.2.2)
(6.2.2)
Optimal position of quantized vectors 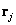 for fixed boundaries of quantization cells, one can find by equating to zero the partial derivatives of quantization errors with respect to the vectors
for fixed boundaries of quantization cells, one can find by equating to zero the partial derivatives of quantization errors with respect to the vectors 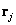 . The result is a system of integral equations.
. The result is a system of integral equations.
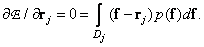 (6.2.3)
(6.2.3)
After transformations we find
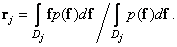 (6.2.4)
(6.2.4)
Equality (6.2.4) defines the conditional expectation of a vector 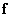 when it enters the cell:
when it enters the cell:
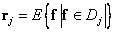 . (6.2.5)
. (6.2.5)
In this case, the minimum mean square quantization error is
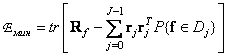 , (6.2.6)
, (6.2.6)
Where 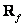 - vector correlation matrix
- vector correlation matrix 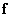 . Note that when
. Note that when 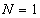 formula (6.2.4) is reduced to (6.1.11), and the expression for quantization error (6.2.6) goes into formula (6.1.12).
formula (6.2.4) is reduced to (6.1.11), and the expression for quantization error (6.2.6) goes into formula (6.1.12).
Optimal positions of quantized vectors 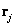 with fixed quantization cells
with fixed quantization cells 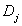 impossible to determine without knowing the joint probability density
impossible to determine without knowing the joint probability density 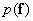 . However, this information is often not available. Another significant difficulty is related to the actual calculation of the integrals in formula (6.2.4). Therefore, it is often necessary to simplify the procedure of vector quantization. So, you can quantize all the components of the vector
. However, this information is often not available. Another significant difficulty is related to the actual calculation of the integrals in formula (6.2.4). Therefore, it is often necessary to simplify the procedure of vector quantization. So, you can quantize all the components of the vector 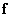 separately, but set quantized vectors
separately, but set quantized vectors 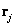 using quantization cells
using quantization cells 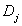 . Then in the three-dimensional space of the cell
. Then in the three-dimensional space of the cell 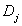 turn into rectangular parallelepipeds. If at the same time the components of the vector
turn into rectangular parallelepipeds. If at the same time the components of the vector 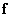 uncorrelated, then vector quantization reduces to sequential quantization of scalar quantities. However, if the samples are correlated, then the problem of determining the optimal vector
uncorrelated, then vector quantization reduces to sequential quantization of scalar quantities. However, if the samples are correlated, then the problem of determining the optimal vector 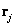 As a rule, it cannot be solved without introducing additional simplifying assumptions. Carey [4] obtained solutions for joint Gaussian densities when quantizing cells
As a rule, it cannot be solved without introducing additional simplifying assumptions. Carey [4] obtained solutions for joint Gaussian densities when quantizing cells 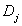 are small enough. Huns [5] investigated a recurrent method for solving such a problem, when each component of a vector is determined using successive approximations based on the remaining quantized components of a vector. This method allows you to find a solution to the problem for many different probability densities: in part 6, it is considered as a means of reducing quantization errors in systems using PCM and transformation coding.
are small enough. Huns [5] investigated a recurrent method for solving such a problem, when each component of a vector is determined using successive approximations based on the remaining quantized components of a vector. This method allows you to find a solution to the problem for many different probability densities: in part 6, it is considered as a means of reducing quantization errors in systems using PCM and transformation coding.
Let us now try to find such a set of quantization cells. 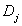 at which the mean square quantization error is minimized. Bruce [6] developed a method for solving this problem based on dynamic programming. However, in the general case, optimal forms of quantization cells are complex and very difficult to determine. Therefore, in most vector quantization methods, a suboptimal approach is used, when for each component of the vector a fixed number of quantization levels is specified.
at which the mean square quantization error is minimized. Bruce [6] developed a method for solving this problem based on dynamic programming. However, in the general case, optimal forms of quantization cells are complex and very difficult to determine. Therefore, in most vector quantization methods, a suboptimal approach is used, when for each component of the vector a fixed number of quantization levels is specified. 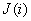 where
where 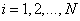 and all components are quantized independently. The optimization problem is reduced in this case to the choice of values
and all components are quantized independently. The optimization problem is reduced in this case to the choice of values 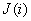 whose work
whose work
 (6.2.7)
(6.2.7)
there is a fixed number of quantization levels for a given vector. Quantization error 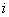 th reference equals
th reference equals
. 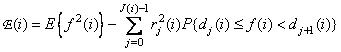 . (6.2.8)
. (6.2.8)
In systems with digital coding, the number of quantization levels is usually chosen equal to the binary number.
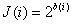 , (6.2.9)
, (6.2.9)
Where 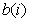 - integer number of code bits (bits) for
- integer number of code bits (bits) for 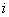 th components of the vector. The total number of code bits must be constant and equal to
th components of the vector. The total number of code bits must be constant and equal to
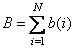 . (6.2.10)
. (6.2.10)
This method of quantization is called block.
Several experts [7-9] have developed algorithms for the distribution of the number of digits. 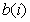 with fixed
with fixed 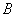 to minimize the root mean square quantization error. When using the algorithm proposed by Redi and Winz [9] and used to quantize independent Gaussian values using the Max method, the following operations should be performed:
to minimize the root mean square quantization error. When using the algorithm proposed by Redi and Winz [9] and used to quantize independent Gaussian values using the Max method, the following operations should be performed:
1. To calculate the distribution of the number of digits by the formula
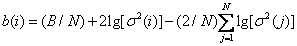 , (6.2.11)
, (6.2.11)
Where 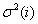 - dispersion
- dispersion 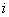 -th countdown.
-th countdown.
2. Round each of the numbers. 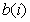 to the nearest integer.
to the nearest integer.
3. Change the distribution obtained until condition (6.2.10) is satisfied
The derivation of relation (6.2.11) is based on the exponential approximation of the dependence (6.1.12), which relates the quantization error 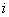 of reference and the number of digits given to it
of reference and the number of digits given to it 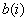 . If a
. If a 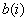 is small, then this approximation turns out to be rather coarse. More reliable results can be obtained using the minimal error method developed by Pratt [10]. Here the digits are successively retracted to the samples that have the largest differential error (6.2.8). When quantizing values with zero mean, the algorithm consists of the following steps:
is small, then this approximation turns out to be rather coarse. More reliable results can be obtained using the minimal error method developed by Pratt [10]. Here the digits are successively retracted to the samples that have the largest differential error (6.2.8). When quantizing values with zero mean, the algorithm consists of the following steps:
Step 1. Determination of the initial conditions:
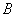 - the total number of digits in the code combination block,
- the total number of digits in the code combination block,
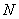 - block length
- block length
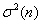 - dispersion components
- dispersion components
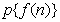 - the probability density of the components
- the probability density of the components
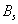 - discharge index (zero first).
- discharge index (zero first).
Step 2. Calculate and remember the differential error coefficients.
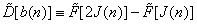 ,
,
Where 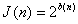 and the amount
and the amount
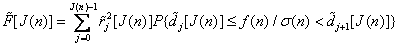
determines the error rate for random variables with unit variance, with the tilde sign (~) marked by quantization levels and threshold levels related to such quantities.
Step 3. Allocate one digit to the component for which the product 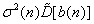 has the greatest value; increase by one
has the greatest value; increase by one 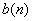 and
and 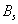 .
.
Step 4. If 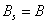 , finish the procedure; otherwise repeat step 3.
, finish the procedure; otherwise repeat step 3.
Differential Error Ratios 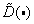 necessary for this algorithm can be calculated in advance and stored as a table from
necessary for this algorithm can be calculated in advance and stored as a table from 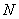 numbers In this case, the algorithm reduces to
numbers In this case, the algorithm reduces to 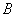 sequential bit allocation operations. The advantages of the algorithm are that it does not require cumbersome calculations, and there are no approximation and rounding errors characteristic of the algorithm with the calculation of the logarithms of the variances. In addition, the minimum error method relies on a probability density model and, therefore, it can be effectively used for the distribution of discharges at different sample probability densities.
sequential bit allocation operations. The advantages of the algorithm are that it does not require cumbersome calculations, and there are no approximation and rounding errors characteristic of the algorithm with the calculation of the logarithms of the variances. In addition, the minimum error method relies on a probability density model and, therefore, it can be effectively used for the distribution of discharges at different sample probability densities.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing