Lecture
Singular operators are widely used in the analysis of two-dimensional systems, especially systems in which discretization of continuous functions is performed. Dirac’s 2D delta function is a singular operator with the following properties:
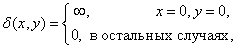 (1.3.1a)
(1.3.1a)
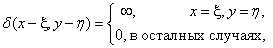 (1.3.1b)
(1.3.1b)
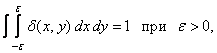 (1.3.1b)
(1.3.1b)
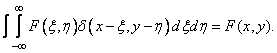 (1.3.1g)
(1.3.1g)
Magnitude 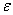 here denotes an infinitesimal limit of integration.
here denotes an infinitesimal limit of integration.
The two-dimensional delta function can be represented as the product of two one-dimensional delta functions of orthogonal coordinates 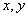 :
:
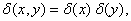 (1.3.2)
(1.3.2)
where one-dimensional delta functions satisfy one-dimensional relations similar to (1.3.1). The delta function can also be defined as the limit of some functions [1, p. 275], for example, a rectangular function
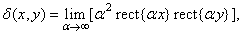 (1.3.3a)
(1.3.3a)
circular function
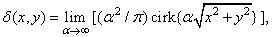 (1.3.3b)
(1.3.3b)
Gaussian function
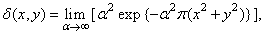 (1.3.3b)
(1.3.3b)
sinc functions
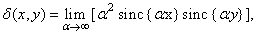 (1.3.3g)
(1.3.3g)
Bessel function
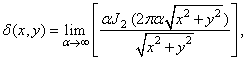 (1.3.3d)
(1.3.3d)
Where
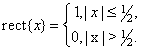 (1.3.4a)
(1.3.4a)
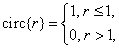 (1.3.4b)
(1.3.4b)
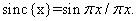 (1.3.4в)
(1.3.4в)
Another useful definition of the delta function is the following identity [2, p. 99]:
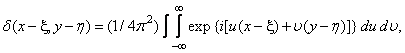 (1.3.5)
(1.3.5)
Where 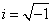 .
.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing