Lecture
The Fourier transform convolution theorem (1.6.14) turns out to be a very useful tool in analyzing linear systems. Consider the function 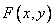 describing the image at the input of the linear system by the simplicity response
describing the image at the input of the linear system by the simplicity response 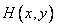 . The output image is described by the function
. The output image is described by the function 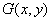 resulting from the convolution:
resulting from the convolution:
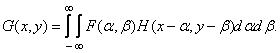 (1.7.1)
(1.7.1)
Performing the Fourier transform of both parts of this equality and changing the order of integration in its right side, we get
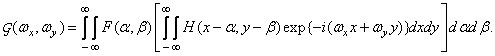 (1.7.2)
(1.7.2)
According to the shift theorem (1.6.13), the inner integral is equal to the product of the spectrum of the function 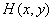 and the exponential phase shift factor. therefore
and the exponential phase shift factor. therefore
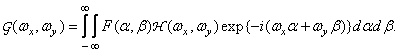 (1.7.3)
(1.7.3)
Having executed Fourier transforms, we get
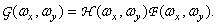 (1.7.4)
(1.7.4)
Finally, the inverse Fourier transform gives a function that describes the output image:
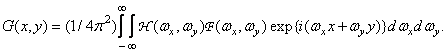 (1.7.5)
(1.7.5)
Expressions (1.7.1) and (1.7.5) represent two alternative ways of determining the output image of a linear spatially invariant system. The choice of one or another approach depends on the problem to be solved.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing