Lecture
An orthogonal transform, called a slant transform, was proposed in [24–26]. This transformation has the following features: 1) among the basis vectors there is a vector with the same components (a constant basis vector); 2) the oblique basis vector monotonically decreases from the maximum to the minimum value by jumps of a constant value; 3) the transformation matrix has a sequential property; 4) there is a fast conversion algorithm; 5) provides a high degree of energy concentration of the image. With the length of the vector 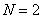 the oblique transform coincides with the Hadamard transform of the second order. In this way,
the oblique transform coincides with the Hadamard transform of the second order. In this way,
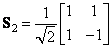 . (10.7.1)
. (10.7.1)
The matrix of the oblique transformation of the fourth order is formed according to the following rule:
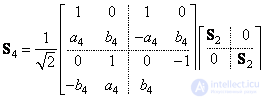 , (10.7.2а)
, (10.7.2а)
or
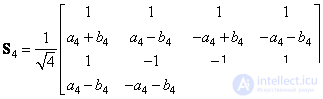 , (10.7.2b)
, (10.7.2b)
Where 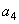 and
and 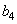 - the actual coefficients that should be chosen so that the matrix
- the actual coefficients that should be chosen so that the matrix 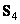 was orthogonal, and the magnitude of the jumps with a change in the second oblique basis vector was constant. From the condition of constancy of the magnitude of the jump, one can find that
was orthogonal, and the magnitude of the jumps with a change in the second oblique basis vector was constant. From the condition of constancy of the magnitude of the jump, one can find that 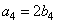 . From the condition of orthogonality
. From the condition of orthogonality 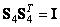 follows that
follows that 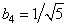 . Thus, the quadratic oblique transformation matrix is
. Thus, the quadratic oblique transformation matrix is
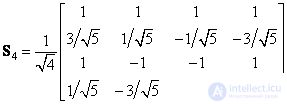 . (10.7.3)
. (10.7.3)
It is easy to check that the matrix 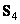 is orthonormal. In addition, it has a sequential property: the number of changes in the sign increases with the line number from 0 to 3.
is orthonormal. In addition, it has a sequential property: the number of changes in the sign increases with the line number from 0 to 3.
Oblique transform matrix when 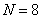 has the appearance
has the appearance
 . (10.7.4)
. (10.7.4)
As in the construction of the matrix 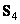 , coefficients
, coefficients 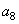 and
and 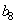 are chosen so that the oblique basis vector decreases in uniform jumps, all rows of the matrix are orthonormal vectors, and the matrix itself has a sequential property.
are chosen so that the oblique basis vector decreases in uniform jumps, all rows of the matrix are orthonormal vectors, and the matrix itself has a sequential property.
Summarizing the relation (10.7.4), one can obtain a recurrent formula connecting the oblique transformation matrices 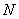 th and
th and 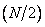 th order:
th order:
 , (10.7.5)
, (10.7.5)
Where 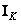 - unit matrix
- unit matrix 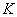 th order. Permanent
th order. Permanent 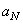 and
and 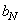 can be found from recurrence relations [26]
can be found from recurrence relations [26]
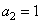 , (10.7.6a)
, (10.7.6a)
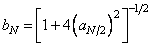 , (10.7.6b)
, (10.7.6b)
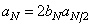 (10.7.6b)
(10.7.6b)
or by the formulas
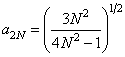 , (10.7.7a)
, (10.7.7a)
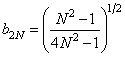 . (10.7.7b)
. (10.7.7b)
In fig. 10.7.1 shows the graphs of the basic functions of the oblique transformation for 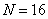 . An example of the spectrum obtained by this transformation is shown in Fig. 10.7.2.
. An example of the spectrum obtained by this transformation is shown in Fig. 10.7.2.
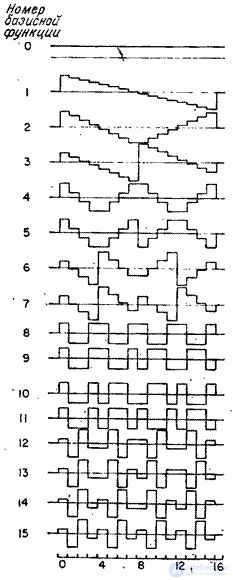
Fig. 10.7.1. Basic functions of the oblique transform 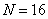 .
.

Fig. 10.7.2. Slanting image conversion "Portrait".
a - the original image; b - the result of the transformation in a logarithmic scale along the axis of amplitudes: c - the result of the transformation with limited greatest harmonics.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing