7.7. SPEED OF CREATING INFORMATION BY THE SOURCE OF IMAGES

The speed at which information is created by some source determines the minimum amount of bandwidth required to transmit a message with a given permissible level of distortion in a received message relative to the transmitted one [45, 46]. A number of attempts were made [2, 47–50] to adapt information theory to image transfer tasks in order to determine the limits of image coding systems. This section contains the main provisions of this theory, formulated in relation to images based on the review article by Davisson [50].

Fig. 7.7.1. Block diagram of the information transmission system.

In fig. 7.7.1 shows a simplified block diagram of an image transmission system. The source creates a sequence of 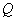image elements, each of which is quantized into 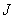levels. This sequence forms a vector 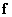size 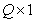. In the coder to each of 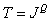possible combinations of brightness 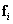where 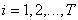The code combination is matched.

After decoding, the combination of brightness is restored 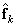. Characteristics of the image transmission system can be described using conditional probability. 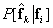of vector 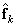, at the output, provided that the vector was encoded . If the encoder and decoder work without errors, then the input and output vectors of the image (in the absence of channel errors) will be the same.

Conditional probability 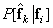describes the operation of the image transmission system in the presence of distortion. Based on this conditional probability and the distribution of a priori probabilities, we find the unconditional probability distribution of the reconstructed vectors

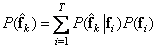. (7.7.1)

Channel capacity requirements are determined by the amount of mutual information, by definition equal to

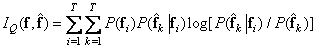. (7.7.2)

With error-free coding, this expression is simplified:

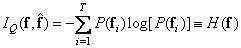, (7.7.3)

that is, the amount of mutual information is equal to the entropy of the source. If in the process of encoding distortions are made, then the recovered sequence contains incomplete status information and bandwidth requirements will be reduced.

Suppose the function 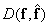is a measure of the distortion of the reproduced image. Then for a vector from 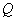elements, the average value of distortion per element will be determined by the equality

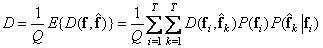. (7.7.4)

We define for this vector the speed of creating information per one element as

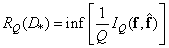(7.7.5)

at 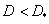. Basically 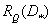and there is a minimum channel capacity necessary to transmit information created by the source, when the distortions on average should not exceed a certain maximum value 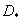. The speed of creating information source 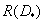can be found by increasing the length of the vector to infinity:

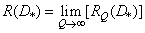. (7.7.6)

As a rule, to find the minimum amount of mutual information, provided that the average value of the distortion should not exceed a specified limit 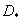difficult both analytical and numerical methods. Received several solutions for communication channels used in practice. One of them relates to a source with a Gaussian probability distribution when estimating the distortions by the mean square measure. This solution cannot be directly applied to the problem of coding the brightness of the elements, since the brightness is a non-negative value. In addition, the rms distortion measure may not be appropriate. However, the solution obtained for the Gaussian source and the rms distortion measure allows one to indicate the limits of the coding system for any sources with given second moments. In addition, this solution is directly transferred to the transformation coding problem. Therefore, below we will consider the properties of the rate of creation of information for the case of a Gaussian source and the mean square distortion measure.

Consider a vector 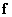educated 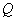independent Gaussian random variables with zero means and known variance 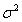. The rms error is determined by the formula

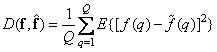. (7.7.7)

It was found [45] that the speed of creating information

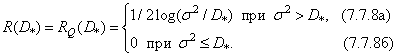
Thus, the rate at which information is created is equal to half the logarithm of the signal power ratio to the distortion power, if this ratio exceeds unity, and zero otherwise. If the elements of the sequence created by the Gaussian source are correlated and the covariance matrix 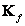known, the speed of creating information is equal to [50]

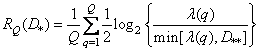, (7.7.9)

Where 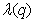- -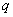e eigenvalue of the matrix 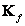, but 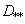chosen so that

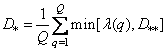. (7.7.10)

In image processing, a special case of a two-dimensional separable Markov source is of interest, when all elements have the same dispersions equal to 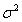and the correlation coefficients along the rows and columns are respectively 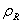and 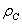. If we assume that the degree of distortion is small, then the speed of creating information for a homogeneous case is [50]

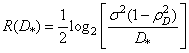, (7.7.11)

and in the two-dimensional case

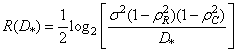. (7.7.12)

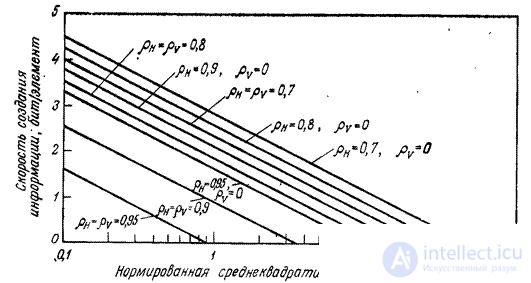
Fig. 7.7.2. The dependence of the rate of creation of information on the magnitude of distortion in one- and two-dimensional coding of images - realizations of the Markov field.

In fig. 7.7.2 shows the graphs of the rate of creation of information on the magnitude of distortion for different values ​​of the correlation coefficients. In ch. 24 a comparison was made of the characteristics of some image coding systems with limiting characteristics.