7.3.2. COLOR METRICS

To determine the color differences, you can enter a deterministic measure, if we consider the color space defined by the three color coordinates as Euclidean space. Then color 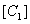given by the values ​​of three coordinates 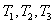will be separated from color 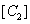with color coordinates 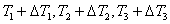by distance 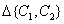determined by the ratio

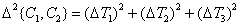. (7.3.9)

If this measure of color difference is consistent with the subjective ideas, then for all values ​​of the color coordinates the same increments 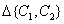must match the same subtle (threshold) color differences. In other words, the equation 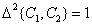should describe the sphere of radius in one threshold unit of color difference with the center at the point 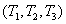. Exceptions are only those points that correspond to pure primary colors — red, green, and blue. Experiments have shown that human vision is most sensitive to single changes in the blue color coordinate, and least sensitive to green [18].

In order to achieve a better fit of measure (7.3.9) with the results of subjective tests, it can be assumed that the color space is Riemannian. By definition, the distance in a Riemannian color space is expressed as

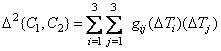, (7.3.10)

where are the coefficients 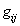are functions 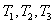. Equating expression (7.3.10) to unity, we obtain the equation of an ellipsoid centered at 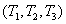. It has been established that colors that are barely noticeably different from this color can be fairly accurately described with ellipsoids in the space of primary colors.

The expression (7.3.10) is used in colorimetry as a measure of color difference, if the distance between them does not exceed several threshold units. If the colors differ more strongly, then the elementary increments along the shortest path connecting the corresponding points of the color space should be summed up. Then the global measure of color difference will be given by

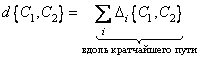(7.3.11)

In Euclidean space, the shortest path is a straight line. In a Riemannian space, the shortest path, called the geodesic line, generally passes along a certain curve. Mut and Pursels [19], as well as Jane [20], compiled programs for calculating the distances between colors, based on the construction of geodesic lines in the color space. Based on these programs, we managed to create a very accurate color space metric, but it takes a lot of time to perform calculations.

It is relatively difficult to use the Riemannian metric (7.3.10), so the question naturally arises whether such a mapping of three-dimensional space exists with coordinates 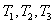on Euclidean three-dimensional space with coordinates 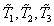in which the color difference metric remains unchanged. In this new space, the color coordinate increments should satisfy the relation

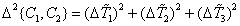, (7.3.12)

so that the surface of subtle colors is a sphere with a center at the point 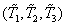. It was shown [16, p. 513] that, in the general case, there is no linear transformation that has exactly the required properties. However, it was found several linear transformations with properties close to the specified. The International Commission on Illumination (ICE) has adopted a coordinate system 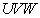based on the work of Judd [21] and McAdam [22]. In this system, the distances between the colors at the threshold of discrimination are almost the same. In fig. 7.3.2, and the results of measurements of barely noticeable differences in colors, made by Mc Adam [23]. The sets of barely distinguishable colors are approximated by ellipses and are represented on the chromaticity graph in coordinates. . If the same data is presented on the graph of chromaticity with coordinates 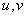(Fig. 7.3.2, b), then the ellipses become closer in size and noticeably rounded. Farnsworth [24] found a non-linear transformation, as a result of which Mac-Adam ellipses (within the limits of the Mac-Adam measurements) turn into circles (Fig. 7.3.3). K. Unfortunately, this transformation is expressed as a complex function of chromaticity coordinates. 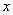and 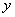and requires cumbersome computation.

In the coordinate system 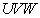the distance between colors is

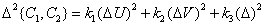, (7.3.13)

Where 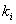- permanent.

The human eye is more sensitive to changing shades of dark colors. In an effort to use this circumstance, the ICE temporarily introduced a coordinate system as standards and in which changes in chromaticity and lightness should be equally noticeable [25]. In these systems, the color difference is determined by the values

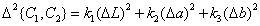, (7.3.14a)

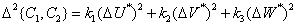. (7.3.14b)

Fig. 7.3.2. Mac-Adam ellipses for threshold color differences in coordinate systems and [23]. The sizes of the ellipses are increased 10 times: a - the graph of chromaticities in the coordinates 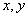; b - graph of chromaticity in coordinates .

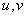One of the drawbacks is the measure of color difference in the 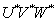is the indistinguishability of the difference in color tone and color saturation. It is believed that differences in color tone are much more noticeable than differences in color saturation. Therefore, a coordinate system was introduced. 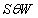, wherein 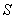in proportion to saturation, and 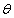- color tone [26, p. 152].

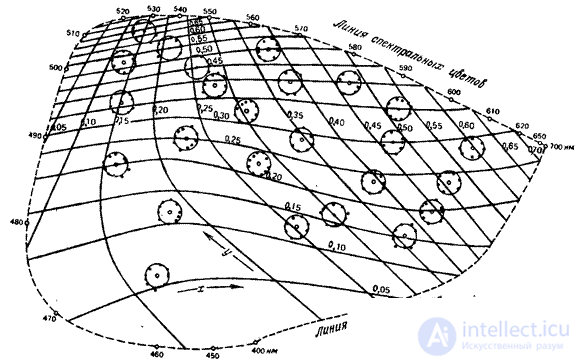
Fig. 7.3.3. Nonlinear transformation of Mac-Adam ellipses on the chromaticity graph in the coordinate system 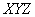[24].

The difference in colors in this system is measured by

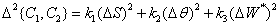. (7.3.15)

If the color has a very weak saturation, i.e., it is close to gray, then changes in the color tone have no special meaning. On this basis, another measure of color difference was introduced [26, p. 152]:

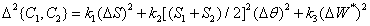. (7.3.16)

All the above formulas are the results of attempts to create a subjectively uniform measure of color differences. There have been few experiments conducted that would allow to determine the value of each of them, so the question of choosing an appropriate measure is still open.