Lecture
Two-dimensional linear transformations can be defined as a series as
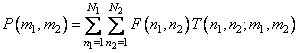 . (11.1.1)
. (11.1.1)
This ratio in vector form is
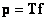 . (11.1.2)
. (11.1.2)
It will be shown below that such linear transformations can often be performed more efficiently if, instead of direct calculations using formulas (11.1.1) or (11.1.2), we use indirect methods using two-dimensional unitary transformations.
In fig. 11.1.1 the block diagram of the indirect method of calculation, called generalized linear filtering [1], is given. Array 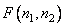 describing the original image, is subjected here to a two-dimensional unitary transformation, which results in an array of transformation coefficients
describing the original image, is subjected here to a two-dimensional unitary transformation, which results in an array of transformation coefficients 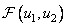 . Then a linear combination of these coefficients is compiled, which is generally described by the formula
. Then a linear combination of these coefficients is compiled, which is generally described by the formula
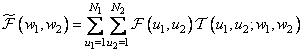 , (11.1.3)
, (11.1.3)
Where 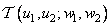 - the core of the linear filtering transformation. Finally, an inverse unitary transformation is performed to obtain the processed image.
- the core of the linear filtering transformation. Finally, an inverse unitary transformation is performed to obtain the processed image. 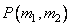 .
.
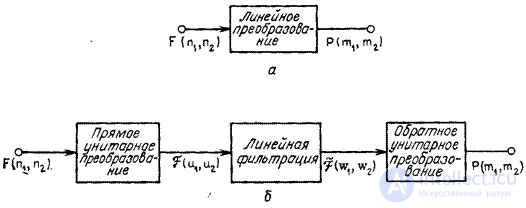
Fig. 11.1.1. The structure of the algorithms for direct processing (a) and generalized linear filtering (b).
Such a calculation method will be more efficient than direct calculation using formula (11.1.1) if there are fast unitary transformation algorithms, and the core 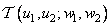 contains a large number of zero elements.
contains a large number of zero elements.
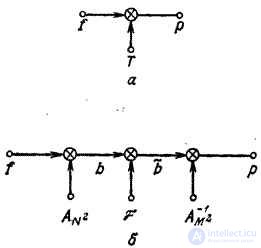
Fig. 11.1.2. The structure of the algorithms for direct processing (a) and generalized linear filtering (b) in the vector representation of images.
The process of generalized linear filtering can also be represented in a vector form (Fig. 11.1.2). To simplify the notation, we assume that 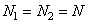 , but
, but  . Then the generalized linear filtering can be described by the relations
. Then the generalized linear filtering can be described by the relations
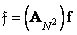 , (11.1.4a)
, (11.1.4a)
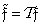 , (11.1.4b)
, (11.1.4b)
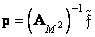 , (11.1.4b)
, (11.1.4b)
Where 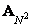 - matrix of unitary size conversion
- matrix of unitary size conversion 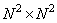 ,
, 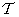 - matrix operator linear size filtering
- matrix operator linear size filtering 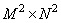 , but
, but 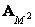 - matrix inverse unitary size conversion
- matrix inverse unitary size conversion 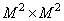 . As follows from relations (11.1.4), the vectors of the original and processed images are related by the equality
. As follows from relations (11.1.4), the vectors of the original and processed images are related by the equality
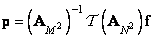 . (11.1.5)
. (11.1.5)
Equating the relations (11.1.2) and (11.1.5), we find the connection between the matrices 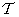 and
and 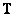 :
:
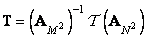 , (11.1.6a)
, (11.1.6a)
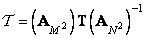 . (11.1.6b)
. (11.1.6b)
For direct processing to perform calculations using the formula (11.1.2), it is necessary to carry out 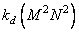 arithmetic action where
arithmetic action where 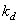
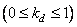 characterizes the degree of filling the matrix
characterizes the degree of filling the matrix 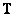 nonzero elements. With generalized linear filtering, the total number of arithmetic operations is:
nonzero elements. With generalized linear filtering, the total number of arithmetic operations is:
Direct conversion:
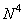 - with direct calculation;
- with direct calculation;
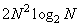 - when using fast conversion.
- when using fast conversion.
Linear filtering:
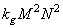 multiplications.
multiplications.
Inverse transform:
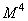 - with direct calculation;
- with direct calculation;
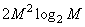 - when using fast conversion.
- when using fast conversion.
Here 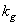
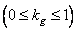 - matrix fill factor
- matrix fill factor  nonzero elements. If a
nonzero elements. If a 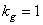 and a direct computation of the unitary transformation is performed, it is obvious that generalized linear filtering is not as effective as direct processing. However, if fast algorithms are used, like the Fast Fourier Transform (FFT), generalized linear filtering will be more efficient than direct processing if the fill factor of the matrix is
and a direct computation of the unitary transformation is performed, it is obvious that generalized linear filtering is not as effective as direct processing. However, if fast algorithms are used, like the Fast Fourier Transform (FFT), generalized linear filtering will be more efficient than direct processing if the fill factor of the matrix is  satisfies inequality
satisfies inequality
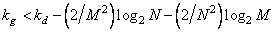 . (11.1.7)
. (11.1.7)
In many cases, the matrix 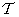 it is sparse and inequality (11.1.7) holds. Generally speaking, unitary transformations often lead to decorrelation of matrix elements.
it is sparse and inequality (11.1.7) holds. Generally speaking, unitary transformations often lead to decorrelation of matrix elements. 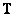 and matrix
and matrix 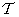 turns out to be sparse. In addition, the matrix
turns out to be sparse. In addition, the matrix 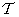 It is often possible to destroy without introducing large errors if we replace its elements with small values by zeros [1].
It is often possible to destroy without introducing large errors if we replace its elements with small values by zeros [1].
In the following sections, the structure of linear superposition, convolution, and pseudo-inversion operators is considered in order to determine the possibility of applying the method of generalized linear filtering to perform these operations.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing