10.4. SINUS TRANSFORMATION

The fast sine transform proposed by Jane [13] as an approximation of the Karhunen-Loeve transform for a Markov process is, in the one-dimensional case, determined using basic functions of the form

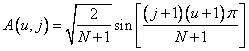, (10.4.1)

Where 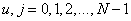. Consider a matrix containing non-zero elements only on the main diagonal and two subdiagonal lines adjacent to it (the so-called three-diagonal matrix):

, (10.4.2)

Where 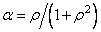, and 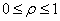- the correlation coefficient of the neighboring elements of the Markov process. It can be shown [141 that using a unitary matrix 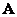, whose elements are basic functions (10.4.1), the matrix 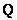can be diagonalized in the sense that

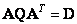, (10.4.3)

Where 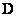- diagonal matrix made up of elements

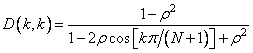(10.4.4)

at .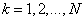

The two-dimensional sinus transform is defined by the ratio

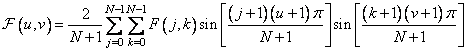, (10.4.5)

and the inverse transform has the same form. The sine transform can be calculated using the Fourier transform algorithm. Assume an array 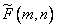by size 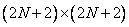formed according to equalities

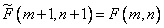at 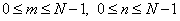, (10.4.6a)

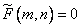in other cases. (10.4.6b)

Then, selecting the imaginary part of the Fourier coefficients of the array 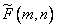, you can find the sinus transform in the form

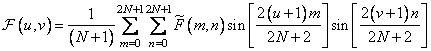. (10.4.7)

Graphs of the basic functions of the sinus transform when 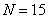are presented on fig. 10.4.1, and in fig. 10.4.2 are the photographs obtained by the sinus transform of the image.

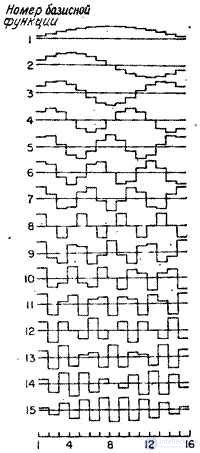
Fig. 10.4.1. Basic functions of the sinus transform when .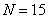

Fig. 10.4.2. Sinus transformation of the image "Portrait".

a - the original image; b - sine spectrum in a logarithmic scale along the amplitude axis; c - spectrum with limited greatest harmonics.