Lecture
Unitary transformations are a special case of linear transformations, when the linear operator [see (8.1.1)] is exactly invertible, and its kernel satisfies the orthogonality conditions [1, 2]. As a result of direct unitary transformation of the image matrix 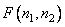 size
size 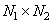 a matrix of the transformed image of the same size is formed, the elements of which by definition are equal
a matrix of the transformed image of the same size is formed, the elements of which by definition are equal
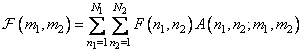 , (10.1.1)
, (10.1.1)
Where 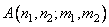 - Direct conversion core. The original image can be obtained using the inverse transform, described by the relation
- Direct conversion core. The original image can be obtained using the inverse transform, described by the relation
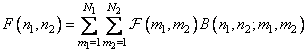 , (10.1.2)
, (10.1.2)
Where 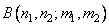 - the core of the inverse transform. A transformation is unitary if the following orthogonality conditions are satisfied:
- the core of the inverse transform. A transformation is unitary if the following orthogonality conditions are satisfied:
 , (10.1.3a)
, (10.1.3a)
 , (10.1.3b)
, (10.1.3b)
 , (10.1.3b)
, (10.1.3b)
 . (10.1.3g)
. (10.1.3g)
A transformation is called separable if both its cores can be represented in the following form:
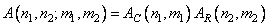 , (10.1.4a)
, (10.1.4a)
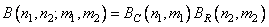 , (10.1.4b)
, (10.1.4b)
where through 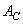 (or
(or 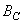 ) and
) and 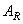 (or
(or 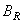 ) denoted respectively the one-dimensional transformation operators of columns and rows. The result of the action of the operator of a separable two-dimensional unitary transformation can be found in two stages. First, a one-dimensional transformation is performed on all the columns of the image matrix, and a matrix with elements is formed
) denoted respectively the one-dimensional transformation operators of columns and rows. The result of the action of the operator of a separable two-dimensional unitary transformation can be found in two stages. First, a one-dimensional transformation is performed on all the columns of the image matrix, and a matrix with elements is formed
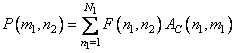 . (10.1.5)
. (10.1.5)
Then a second one-dimensional transformation is performed over all rows of the resulting matrix, which results in the formation of an array of numbers of the form
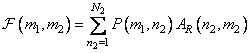 . (10.1.6)
. (10.1.6)
Unitary transformations are conveniently written using vector notation [3]. Assume that 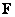 and
and 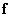 - matrix and vector representation of the array of samples of the original image, and
- matrix and vector representation of the array of samples of the original image, and 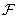 and
and 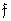 - matrix and vector representations of the transformed image. Then a two-dimensional unitary transformation in vector form is expressed by the relation
- matrix and vector representations of the transformed image. Then a two-dimensional unitary transformation in vector form is expressed by the relation
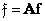 , (10.1.7)
, (10.1.7)
Where 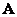 - direct conversion matrix. The inverse transform is written as
- direct conversion matrix. The inverse transform is written as
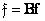 (10.1.8)
(10.1.8)
Where 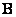 - inverse transformation matrix. It's obvious that
- inverse transformation matrix. It's obvious that
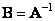 . (10.1.9)
. (10.1.9)
For unitary transformations, the inverse matrix satisfies the relation
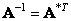 . (10.1.10)
. (10.1.10)
In this case, the matrix 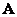 called unitary. A real unitary matrix is called an orthogonal matrix, and for it the relation
called unitary. A real unitary matrix is called an orthogonal matrix, and for it the relation
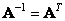 . (10.1.11)
. (10.1.11)
If the transform kernels are separable, so
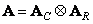 , (10.1.12)
, (10.1.12)
Where 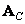 and
and 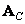 - unitary transformation matrices in rows and columns, then the matrix of the transformed image can be obtained from the matrix of the original image using equality
- unitary transformation matrices in rows and columns, then the matrix of the transformed image can be obtained from the matrix of the original image using equality
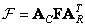 . (10.1.13a)
. (10.1.13a)
The inverse transform is determined by the ratio
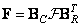 , (10.1.13b)
, (10.1.13b)
Where 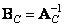 and
and 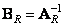 .
.
Separable unitary transformations can also be represented as a weighted sum of the matrix products of column vectors formed from matrix elements. Let be 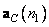 and
and 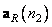 designate
designate 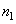 th and
th and 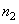 matrix columns
matrix columns 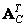 and
and 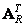 . It is not difficult to show that
. It is not difficult to show that
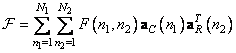 . (10.1.14a)
. (10.1.14a)
Similarly
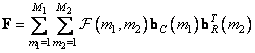 , (10.1.14b)
, (10.1.14b)
Where 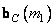 and
and 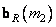 -
- 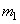 th and
th and 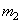 matrix columns
matrix columns 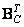 and
and 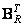 respectively. Matrix products of vectors included in sums (10.1.14) form sequences of matrices, called basic matrices, on the basis of which the matrix is decomposed
respectively. Matrix products of vectors included in sums (10.1.14) form sequences of matrices, called basic matrices, on the basis of which the matrix is decomposed 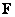 original image or converted image
original image or converted image 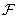 .
.
Various interpretations of unitary transformations are possible. Image transformation can be considered as the decomposition of the original image into a generalized two-dimensional spectrum [4]. Each spectral component characterizes the contribution of the corresponding spectral (basic) function to the energy of the original image. With this interpretation, the concept of frequency can be generalized so that it is applicable not only to sines and cosines, but also to other functions on which the transformations are based. Such a generalized spectral analysis is useful for studying those specific expansions that are most suitable for this class of images. A visual representation of the transformation of images can be obtained in a different way, considering the transformation as a rotation of the multidimensional coordinate system. One of the main properties of the unitary transformation is the preservation of the metric. For example, the Euclidean distance between two images is equal to the Euclidean distance between their images. The third possibility of interpreting transformations is that equality (10.1.2) can be considered as a method of composing an image from a set of two-dimensional functions 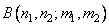 each of which corresponds to a specific point
each of which corresponds to a specific point 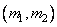 plane of generalized frequencies. In a similar interpretation, the core
plane of generalized frequencies. In a similar interpretation, the core 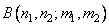 called the two-dimensional basis function, and the coefficient
called the two-dimensional basis function, and the coefficient  indicates the "weight" of this basic function, necessary for obtaining the image in question.
indicates the "weight" of this basic function, necessary for obtaining the image in question.
To simplify the analysis of the properties of two-dimensional unitary transformations, later in this chapter it will be assumed that all arrays are square and have the size 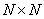 . In addition, the designations and numbering of all indexes in expressions of the form (10.1.1) and (10.1.2) will be changed. Thus, an array of samples of the original image will be denoted by
. In addition, the designations and numbering of all indexes in expressions of the form (10.1.1) and (10.1.2) will be changed. Thus, an array of samples of the original image will be denoted by 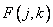 where
where 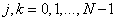 , and an array of conversion factors - through
, and an array of conversion factors - through 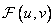 where
where 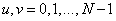 . With this in mind, the direct unitary transformation is written in the following form:
. With this in mind, the direct unitary transformation is written in the following form:
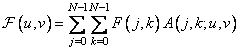 (10.1.15a)
(10.1.15a)
and the inverse transform is like
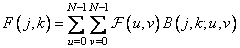 . (10.1.15b)
. (10.1.15b)
Comments
To leave a comment
Digital image processing
Terms: Digital image processing