Lecture
It is known that any matrix 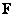 size
size 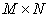 having rank
having rank 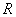 can be represented as a weighted sum of matrices of unit size
can be represented as a weighted sum of matrices of unit size 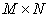 . Such a representation is called singular decomposition [6–8]. The following sections will discuss the use of this method for image processing.
. Such a representation is called singular decomposition [6–8]. The following sections will discuss the use of this method for image processing.
When singular decomposition using a unitary matrix 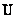 size
size 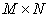 and unitary matrix
and unitary matrix 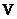 size
size 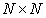 such that
such that
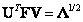 , (5.2.1)
, (5.2.1)
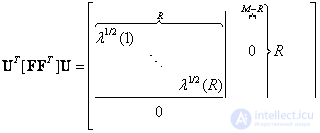
where is the matrix
 (5.2.2)
(5.2.2)
measures 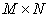 and its diagonal elements
and its diagonal elements 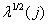 are called singular values of the matrix
are called singular values of the matrix 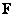 . Since the matrices
. Since the matrices 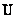 and
and 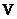 unitary then
unitary then  and
and 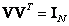 . therefore
. therefore
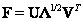 . (5.2.3)
. (5.2.3)
Columns of the unitary matrix 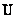 are eigenvectors
are eigenvectors 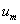 symmetric matrix
symmetric matrix 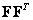 i.e.
i.e.
 (5.2.4)
(5.2.4)
Where 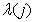 - nonzero eigenvalues of the matrix
- nonzero eigenvalues of the matrix 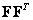 . Similar to the matrix row
. Similar to the matrix row 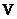 are eigenvectors
are eigenvectors 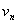 symmetric matrix
symmetric matrix 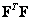 i.e.
i.e.
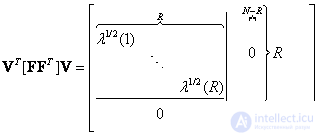 (5.2.5)
(5.2.5)
Where 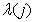 - the corresponding nonzero eigenvalues of the matrix
- the corresponding nonzero eigenvalues of the matrix 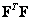 . It is easy to verify that equality (5.2.3) is consistent with (5.2.4) and (5.2.5).
. It is easy to verify that equality (5.2.3) is consistent with (5.2.4) and (5.2.5).
Matrix decomposition 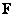 given by relation (5.2.3) can be represented as a series
given by relation (5.2.3) can be represented as a series
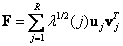 . (5.2.6)
. (5.2.6)
Matrix products of eigenvectors 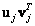 form a set of matrices of unit rank, each of which is multiplied by a weighting factor, which is the corresponding singular value of the matrix
form a set of matrices of unit rank, each of which is multiplied by a weighting factor, which is the corresponding singular value of the matrix 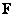 . The consistency of decomposition (5.2.6) with the above relations can be shown by substituting it into equality (5.2.1). The result is
. The consistency of decomposition (5.2.6) with the above relations can be shown by substituting it into equality (5.2.1). The result is
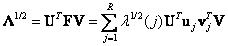 . (5.2.7)
. (5.2.7)
Note that the product 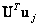 gives a column vector
gives a column vector 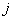 element of which is equal to one, and all the others are zeros. The row vector resulting from the calculation of the product
element of which is equal to one, and all the others are zeros. The row vector resulting from the calculation of the product 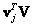 , has a similar look. Therefore, in the right-hand side of (5.2.7), a diagonal matrix is formed, whose elements are equal to the singular values of the matrix
, has a similar look. Therefore, in the right-hand side of (5.2.7), a diagonal matrix is formed, whose elements are equal to the singular values of the matrix 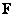 .
.
The matrix expansion (5.2.3) and the equivalent representation in the form of a series (5.2.6) can be found for any matrix. Therefore, such a decomposition can be directly applied to the processing of discrete images presented in the form of matrices. In addition, these formulas can be used to decompose matrices of linear image transformations. The use of the singular value decomposition method for correcting and encoding images is discussed in subsequent chapters of the book.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing