Content
- Introduction
- Time sampling. Discrete signal spectrum
- The repetition of the signal in time. Discrete Fourier Transform
- Inverse Discrete Fourier Transform
- Indexing spectral samples. Rearrangement of spectral samples
- findings
Introduction
Fourier analysis today is without doubt the most common analysis tool that is used in all branches of science and technology. However, before the advent of computers, the discrete Fourier transform (DFT) was rarely used, since the calculation of the DFT of 32 samples requires 1024 operations of complex multiplication and addition, which in manual count for quite a long time. However, the first mention of the fast Fourier transform algorithm refers to the work of Gauss, in which he used the periodicity properties of trigonometric functions to calculate the DFT. However, no one paid attention to this work for a long time, until personal computers were widely used.
The first software implementation of the FFT algorithm was carried out in the early 60s of the 20th century by John Cooley at the IBM computer center under the supervision of Tesca John Tukey, and in 1965 they themselves published an article on the Fast Fourier Transform algorithm. From this moment begins the real FFT-mania. Thousands of papers devoted to the FFT algorithm are published, monographs are published one by one, programmers compete in the efficiency of the algorithm implementation. FFT becomes the main tool for spectral analysis of signals.
The principle of construction of algoritm FFT
What gave impetus to this rapid development? Consider the expression for the discrete Fourier transform:
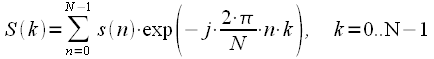 . . |
(one) |
DFT
signal readings
(generally complex) puts in compliance
complex spectrum readings
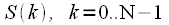
, and to calculate a single spectral reference is required
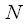
operations of complex multiplication and addition. Thus, the computational complexity of the DFT algorithm is
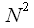
complex multiplications and additions. In this case, it can be noted that if one DFT on
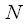
points (counts) to replace the calculation of two DFT on
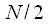
points, this will reduce the number of operations by 2 times. Replacement
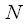
-point DFT two
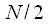
-point presented in Figure 1.
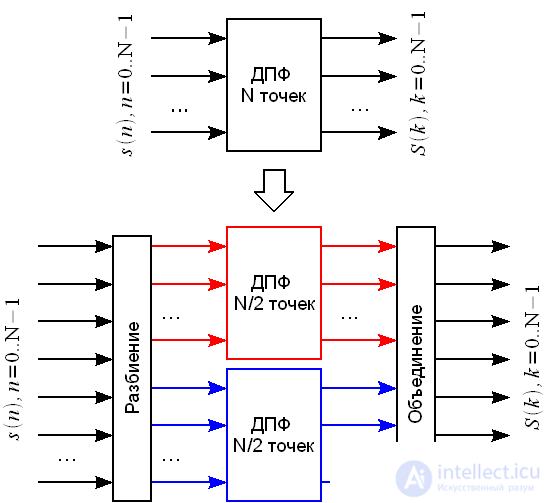
Figure 1: Replacing the N-point DFT with two N / 2-point DFT
In addition, each of
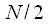
- point DFT can also be calculated by replacing
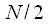
-point DFT for two
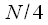
-point. In this case, the number of computational operations is equal to
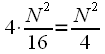
. In this way, it is possible to continue splitting the source sequence as long as it is possible to divide the sequence into two. Obviously, if
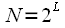
,
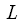
- positive integer, we can split the sequence in half
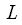
time. For
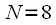
(
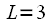
) such a partition is presented in Figure 2.
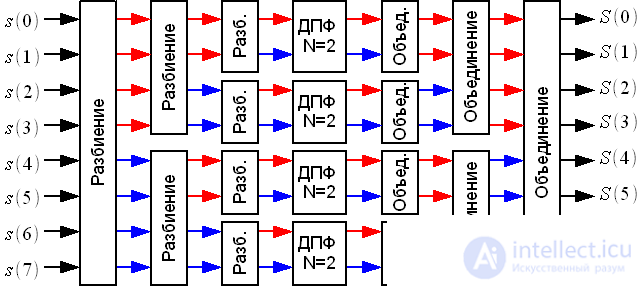
Figure 2: Splitting and combining sequences with N = 8
Each partition divides the sequence into two half-lengths (red and blue), and each join “assembles” one of the doubled lengths from the two sequences.
FFT algorithms that use length samples
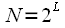
are called “base 2 FFT algorithms”. These algorithms are the most common, due to the fact that in machine arithmetic
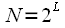
is a “round” number. Further, we will consider only the algorithms for base 2.
Obviously, it is possible to divide the sequence into two differently, but it depends on whether we can get an undistorted signal spectrum when combined and what it will cost us in terms of computational costs. It can be said that the efficiency of the FFT algorithm depends entirely on the method of splitting and combining the sequence, since if we disregard the operations on splitting-combining, then to calculate the spectrum is required
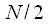
calculate the DFT times by 2 points, as a result, the total number of computational operations will be
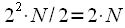
, that is, the number of operations linearly depends on the size of the sample.
We consider two ways of splitting - combining: thinning by time and thinning by frequency. An example of software implementation and use of the FFT algorithm will also be given.
Before considering the methods of splitting - combining, we need to consider the inverse discrete Fourier transform (IDFT):
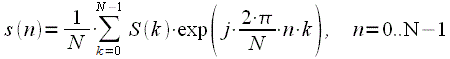 , , |
(2) |
which puts in line
complex spectrum readings
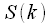
,
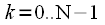
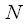
complex signal values
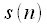
,
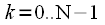
.
Inverse Fast Fourier Transform
Having an FFT calculation algorithm, I would very much like to use it for the inverse transformation. To do this, pay attention to the fact that:
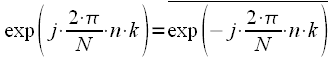 . . |
(3) |
In other words, the complex exponentials in the expression for the direct and inverse DFT are complex conjugate (the bar above means complex conjugation). Now consider two complex numbers
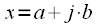
and
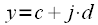
.
Consider the product
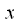
on complex conjugate
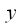
:
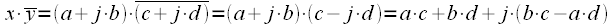 . . |
(four) |
Now consider the product of complex conjugate
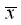
on
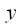
:
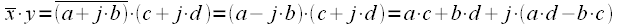 . . |
(five) |
Comparing (4) and (5) we can conclude:
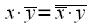 . . |
(6) |
With reference to the expression of IDFT, you can write:
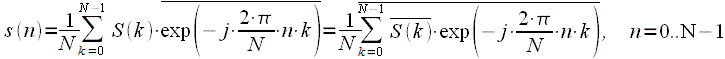 |
(7) |
Thus, a complex conjugate spectrum is taken.
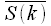
the direct DFT is performed and the result is subjected to complex conjugation. Calculation of ODP with the use of DFT is shown in Figure 3.
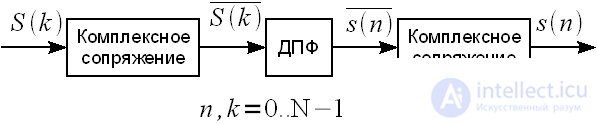
Figure 3: Calculation of the inverse DFT through direct
If instead of the DFT we use the FFT, then we obtain the inverse fast Fourier transform (OBFT). In this case, to perform complex conjugation, it is only necessary to change the sign in front of the imaginary part of the spectrum before calling the FFT function and the result after the FFT.
findings
Thus, we considered the way of acceleration of calculations in the calculation of the DFT, and also reduced the IDFT to a direct one. Now it is necessary to consider partitioning methods — unions that provide a significant reduction in computations. In the following articles, we will examine in detail the FFT algorithms for base two with decimation by time and frequency by frequency.
 .
. signal readings
signal readings 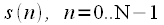 (generally complex) puts in compliance
(generally complex) puts in compliance 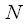 complex spectrum readings
complex spectrum readings 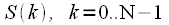 , and to calculate a single spectral reference is required
, and to calculate a single spectral reference is required 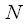 operations of complex multiplication and addition. Thus, the computational complexity of the DFT algorithm is
operations of complex multiplication and addition. Thus, the computational complexity of the DFT algorithm is 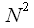 complex multiplications and additions. In this case, it can be noted that if one DFT on
complex multiplications and additions. In this case, it can be noted that if one DFT on 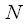 points (counts) to replace the calculation of two DFT on
points (counts) to replace the calculation of two DFT on 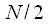 points, this will reduce the number of operations by 2 times. Replacement
points, this will reduce the number of operations by 2 times. Replacement 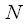 -point DFT two
-point DFT two 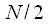 -point presented in Figure 1.
-point presented in Figure 1.
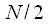 - point DFT can also be calculated by replacing
- point DFT can also be calculated by replacing 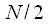 -point DFT for two
-point DFT for two 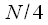 -point. In this case, the number of computational operations is equal to
-point. In this case, the number of computational operations is equal to 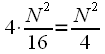 . In this way, it is possible to continue splitting the source sequence as long as it is possible to divide the sequence into two. Obviously, if
. In this way, it is possible to continue splitting the source sequence as long as it is possible to divide the sequence into two. Obviously, if 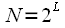 ,
, 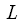 - positive integer, we can split the sequence in half
- positive integer, we can split the sequence in half 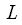 time. For
time. For 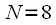 (
( 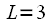 ) such a partition is presented in Figure 2.
) such a partition is presented in Figure 2.
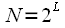 are called “base 2 FFT algorithms”. These algorithms are the most common, due to the fact that in machine arithmetic
are called “base 2 FFT algorithms”. These algorithms are the most common, due to the fact that in machine arithmetic 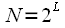 is a “round” number. Further, we will consider only the algorithms for base 2.
is a “round” number. Further, we will consider only the algorithms for base 2.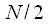 calculate the DFT times by 2 points, as a result, the total number of computational operations will be
calculate the DFT times by 2 points, as a result, the total number of computational operations will be 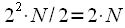 , that is, the number of operations linearly depends on the size of the sample.
, that is, the number of operations linearly depends on the size of the sample.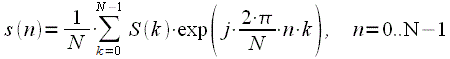 ,
,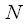 complex spectrum readings
complex spectrum readings 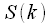 ,
, 
 complex signal values
complex signal values 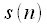 ,
, 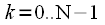 .
.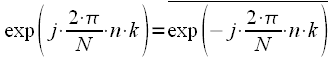 .
.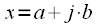 and
and 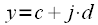 .
.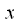 on complex conjugate
on complex conjugate 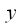 :
: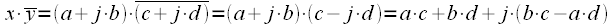 .
.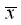 on
on 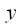 :
: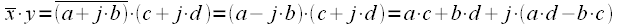 .
.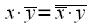 .
.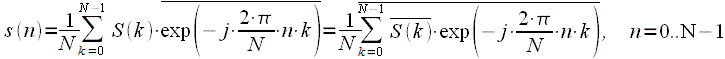
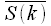 the direct DFT is performed and the result is subjected to complex conjugation. Calculation of ODP with the use of DFT is shown in Figure 3.
the direct DFT is performed and the result is subjected to complex conjugation. Calculation of ODP with the use of DFT is shown in Figure 3.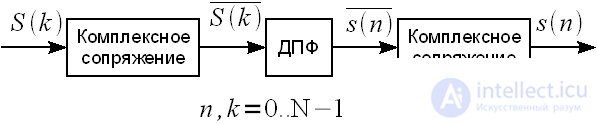
Comments
To leave a comment
Digital signal processing
Terms: Digital signal processing