Lecture
The Hadamard transform [16, 17] is based on the Hadamard square matrix [18], the elements of which are equal to plus or minus one, and the rows and columns form orthogonal vectors. Normalized Hadamard Matrix 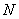 th order satisfies the relation
th order satisfies the relation
 . (10.5.1)
. (10.5.1)
Among the Hadamard orthonormal matrices, the second-order matrix is the smallest
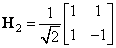 . (10.5.2)
. (10.5.2)
It is known that if the Hadamard matrix is of order 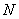 (Where
(Where 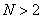 ) exists then
) exists then 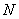 divided by 4 without remainder [19]. It has not yet been possible to determine whether Hadamard matrices exist for arbitrary
divided by 4 without remainder [19]. It has not yet been possible to determine whether Hadamard matrices exist for arbitrary 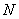 satisfying this condition, but for almost all admissible
satisfying this condition, but for almost all admissible 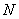 reaching 200, found the rules for constructing the corresponding matrices. It is most easy to construct such matrices with
reaching 200, found the rules for constructing the corresponding matrices. It is most easy to construct such matrices with 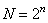 where
where 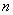 - whole. If a
- whole. If a 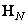 - Hadamard matrix
- Hadamard matrix 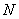 th order, then the matrix
th order, then the matrix
 (10.5.3)
(10.5.3)
is also a Hadamard matrix, but order 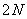 . In fig. 10.5.1 shows the Hadamard matrices of the fourth and eighth order, constructed using the relation (10.5.3).
. In fig. 10.5.1 shows the Hadamard matrices of the fourth and eighth order, constructed using the relation (10.5.3).
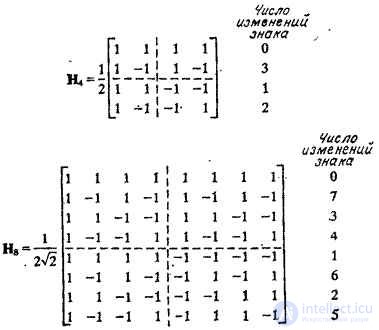
Fig. 10.5.1. Fourth and eighth unordered Hadamard matrices.
Harmut [20] proposed a frequency interpretation of Hadamard matrices having a block structure (10.5.3). The number of sign changes along each row of the Hadamard matrix, divided by two, is called the sequence row. You can build a Hadamard matrix of order 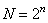 in which the number of character changes in the lines takes values from 0 to
in which the number of character changes in the lines takes values from 0 to 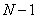 . Unitary matrices with such characteristics are called matrices with the sequential property.
. Unitary matrices with such characteristics are called matrices with the sequential property.
The rows of the Hadamard matrix, described by the relation (10.5.3), can be considered as a sequence of samples of rectangular periodic oscillations (signals) whose period is a multiple of 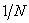 . Such continuous functions, called Walsh functions [21], are associated with impulse Rademacher functions [22]. Consequently, the Hadamard matrix describes the transformation associated with the expansion of functions in a family of rectangular basis functions, and not in sines and cosines characteristic of the Fourier transform.
. Such continuous functions, called Walsh functions [21], are associated with impulse Rademacher functions [22]. Consequently, the Hadamard matrix describes the transformation associated with the expansion of functions in a family of rectangular basis functions, and not in sines and cosines characteristic of the Fourier transform.
For symmetric Hadamard matrices of order 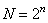 the two-dimensional Hadamard transform can be represented as a series
the two-dimensional Hadamard transform can be represented as a series
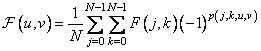 , (10.5.4)
, (10.5.4)
Where
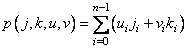 . (10.5.5)
. (10.5.5)
Variables 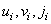 and
and 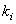 equal to the numbers in the binary representation of numbers
equal to the numbers in the binary representation of numbers 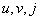 and
and 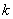 respectively. So for example, if
respectively. So for example, if 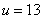 then
then 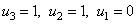 and
and 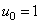 . If the Hadamard matrix is ordered, that is, its rows are rearranged in ascending order of the sequence, then there is another form of the Hadamard transform. In this case
. If the Hadamard matrix is ordered, that is, its rows are rearranged in ascending order of the sequence, then there is another form of the Hadamard transform. In this case
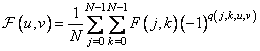 , (10.5.6)
, (10.5.6)
Where
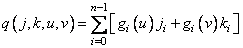 , (10.5.7)
, (10.5.7)
and
 (10.5.8)
(10.5.8)
Graphs of basis functions of the Hadamard transform with an ordered matrix for 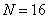 are presented on fig. 10.5.2. Basic images formed with the help of the matrix product of basic Hadamard transform vectors of size
are presented on fig. 10.5.2. Basic images formed with the help of the matrix product of basic Hadamard transform vectors of size 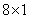 shown in Fig. 10.5.3. In fig. 10.5.4 gives an example of the Hadamard transform (for an ordered Hadamard matrix).
shown in Fig. 10.5.3. In fig. 10.5.4 gives an example of the Hadamard transform (for an ordered Hadamard matrix).
Fig. 10.5.2. Hadamard transform basis functions with 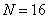 .
.

Fig. 10.5.3. Hadamard transform baseline images 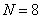 .
.
Black color corresponds to the value +1, white - value -1.

Fig. 10.5.4. Hadamard transform image "Portrait".
a - the original image; b - Hadamard spectrum in a logarithmic scale along the amplitude axis; c - spectrum with limited highest harmonics
Comments
To leave a comment
Digital image processing
Terms: Digital image processing