Lecture
Great attention was paid to the construction and development of a system of quantitative measures of fidelity for reproducing monochrome images [27-32]. Reasonable measures of loyalty should be in good agreement with the results of subjective assessments for a wide class of images, without requiring too complicated calculations. In addition, it is desirable that these measures have a simple analytical form and can be used as criteria for optimality in optimizing or choosing the parameters of image processing systems.
Quantitative measures of fidelity of reproduction of monochrome images can be divided into two groups: single and pair. A single measure is a number that is mapped to any image based on an analysis of its structure. The pair measure is the numerical result of the mutual comparison of two images.
Fidelity measurements in a digital image processing system can be carried out using either a continuous image formed from an array of samples or this array itself. Usually prefer the second method, as it is easier from a practical point of view. However, in order for the measurements on the sample array to be consistent with the results of the subjective assessments, the reproducing device should not create large or at least unpredictable image distortions. Below, we first introduce measures of image fidelity, obtained on the basis of continuous two-dimensional functions, and then present their discrete variants and describe the relationship between them.
Consider a continuous function 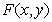 describing an image that is defined in a rectangular area
describing an image that is defined in a rectangular area 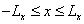 ,
, 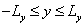 . Suppose that this function is obtained by two-dimensional interpolation of an array of image samples
. Suppose that this function is obtained by two-dimensional interpolation of an array of image samples 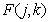
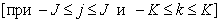 according to the ratio
according to the ratio
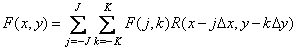 , (7.4.1)
, (7.4.1)
Where 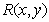 - continuous interpolation function, and
- continuous interpolation function, and 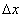 and
and 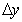 - discretization steps.
- discretization steps.
A single assessment of loyalty in general can be represented by the ratio
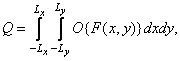 (7.4.2)
(7.4.2)
Where 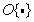 - some (possibly non-linear) operator. Loyalty criteria are often formulated using Fourier transforms. In this case, the generalized form of a single measure of fidelity is
- some (possibly non-linear) operator. Loyalty criteria are often formulated using Fourier transforms. In this case, the generalized form of a single measure of fidelity is
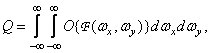 (7.4.3)
(7.4.3)
Where 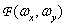 - continuous two-dimensional Fourier spectrum of the image
- continuous two-dimensional Fourier spectrum of the image 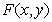 . One of the simplest measures of this kind is the relation proposed by Strehl [33, p. 461].
. One of the simplest measures of this kind is the relation proposed by Strehl [33, p. 461].
 (7.4.4)
(7.4.4)
Where 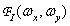 - the spectrum of the original image. Initially, this relationship was used to assess the quality of elements of optical systems. The spectral components of an optical image in some real optical system usually decrease in size and, possibly, change in phase compared to the same components in an ideal (non-aberrational) optical system, the properties of which are limited only by diffraction phenomena. Components with high spatial frequencies, as a rule, are weakened to the greatest extent. Given the definition of the Fourier transform (1.6.6a), the Strehl ratio (7.4.4) reduces to
- the spectrum of the original image. Initially, this relationship was used to assess the quality of elements of optical systems. The spectral components of an optical image in some real optical system usually decrease in size and, possibly, change in phase compared to the same components in an ideal (non-aberrational) optical system, the properties of which are limited only by diffraction phenomena. Components with high spatial frequencies, as a rule, are weakened to the greatest extent. Given the definition of the Fourier transform (1.6.6a), the Strehl ratio (7.4.4) reduces to 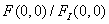 , i.e., to the ratio of the central samples of real and ideal images. Thus, the Strehl ratio is essentially a simple measure for reducing the contrast of a real image compared to the ideal one. The relation of Strehle to some extent corresponds to the subjective ideas about image quality, but experiments show that this correspondence is not always complete. In particular, there are examples of images that have a sufficiently high decipherment, despite the fact that the Strehl ratio for them was small [34].
, i.e., to the ratio of the central samples of real and ideal images. Thus, the Strehl ratio is essentially a simple measure for reducing the contrast of a real image compared to the ideal one. The relation of Strehle to some extent corresponds to the subjective ideas about image quality, but experiments show that this correspondence is not always complete. In particular, there are examples of images that have a sufficiently high decipherment, despite the fact that the Strehl ratio for them was small [34].
Another classic example of a single measure of image fidelity is the equivalent transmittance rectangle, equal by definition [35]
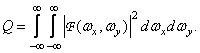 (7.4.5)
(7.4.5)
When squared, the weight of image components with low spatial frequencies increases, as they tend to be large. However, this measure is also not very consistent with the results of subjective tests.
Attempts to create a pair of image quality measures were somewhat more successful. Consider a pair of images consisting of some reference (or ideal) image. 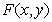 and its distorted version
and its distorted version 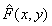 . One of the measures of “proximity” of two images is their mutual correlation, which by definition is equal to
. One of the measures of “proximity” of two images is their mutual correlation, which by definition is equal to
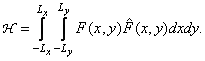 (7.4.6)
(7.4.6)
Usually the cross-correlation is normalized relative to the energy of the reference image so that its maximum value is equal to one. The normalized inter-correlation measure - the correlation coefficient - has the form
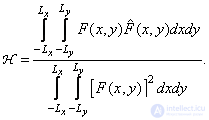 (7.4.7)
(7.4.7)
According to Parseval's theorem (1.6.16), the values of the correlation coefficient can be calculated from the spectra based on the relation
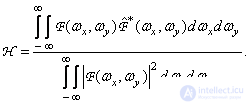 (7.4.8)
(7.4.8)
In the perception of images important role played by the contours of objects. Therefore, Andrews [36] proposed using the correlation coefficient of the Laplacians of images, defined as
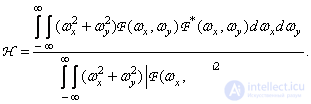 (7.4.9)
(7.4.9)
Recall that by virtue of the relation (1.6.19) the multiplication of the spectrum 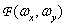 the square of the frequency is equivalent to the use of the Laplace operator, which leads to an aggravation of the contours of the image described by the function
the square of the frequency is equivalent to the use of the Laplace operator, which leads to an aggravation of the contours of the image described by the function 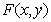 . Experiments performed by Andrews on images that were transformed using low and high spatial frequency filters show that the usual correlation coefficient remains quite large even when the high and medium frequency components of the image are very strongly suppressed and subjectively perceived as low quality. and the correlation coefficient of the Laplacians decreases rapidly as the low-pass filter narrows. It is possible, however, to obtain low-quality images with large distortions in the region of low spatial frequencies, for which the correlation coefficient of the Laplacians is relatively large.
. Experiments performed by Andrews on images that were transformed using low and high spatial frequency filters show that the usual correlation coefficient remains quite large even when the high and medium frequency components of the image are very strongly suppressed and subjectively perceived as low quality. and the correlation coefficient of the Laplacians decreases rapidly as the low-pass filter narrows. It is possible, however, to obtain low-quality images with large distortions in the region of low spatial frequencies, for which the correlation coefficient of the Laplacians is relatively large.
Another paired criterion for image fidelity is the normalized absolute error — the difference between the functions describing the reference and distorted images:
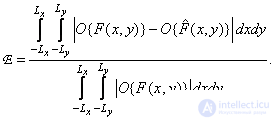 (7.4.10)
(7.4.10)
In image processing, the normalized root-mean-square error, equal to
 (7.4.11)
(7.4.11)
In practice, it is usually preferred to use the root-mean-square rather than the absolute error, since the former is more convenient for analysis than the latter. That is why an intensive search for such transformations was carried out, under which the mean-square error of the transformed function would be well coordinated with the subjective evaluations. Basically, of course, spatial linear and elementwise nonlinear transformations were considered. Quite a lot of attention was paid to power and logarithmic transformations. The operators of linear spatial transformations, such as the gradient operator, the Laplace operator, and the convolution operator, were investigated. In addition, combinations of the aforementioned elementwise and spatial transformations were considered.
The expression for the error can also be represented using spectral characteristics. In this case, the normalized root-mean-square error is determined by the ratio
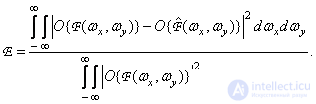 (7.4.12)
(7.4.12)
An interesting special case of a linear transform is frequency weighting when
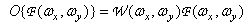 , (7.4.13)
, (7.4.13)
Where 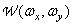 - weight function. The expression for the frequency-weighted root-mean-square error is obtained as
- weight function. The expression for the frequency-weighted root-mean-square error is obtained as
 . (7.4.14)
. (7.4.14)
It should be noted that the formula (7.4.14) is completely equivalent to the expression (7.4.11) for the root-mean-square error, if the operator 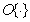 corresponds to the convolution performed by a linear filter with frequency response
corresponds to the convolution performed by a linear filter with frequency response
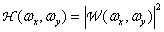
Wilder [37] conducted a deep study of the properties of absolute and root-mean-square errors in a discrete form in relation to power, logarithmic and gradient transformations, as well as to the Laplace transform. Distorted image samples were obtained by modeling the coding process of the original image using various algorithms. It was found that the element-by-element transformations in combination with the criteria of absolute and root-mean-square errors do not allow one to obtain a criterion of fidelity consistent with subjective evaluations. Measures of error, based on the Laplace transform and gradient transformation, have the greatest correlation with the subjective evaluations, but the correlation coefficient does not exceed 0.8, i.e., these criteria are not sufficiently reliable.
Most attempts to find acceptable criteria for image fidelity refer to particular cases. A certain criterion is proposed, based on some physiological assumptions, and more often simply convenient for analysis and calculations, and then its properties are evaluated. Another approach to the problem is to copy the process of developing a human assessment, that is, the properties of the image should be measured in the metric that is inherent in the human brain. With this approach, the estimated image first undergoes preliminary processing and only then its fidelity is evaluated. In this case, as far as possible, processes that actually occur in the initial links of the human visual system are approximated. In ch. 2, a model of the input cascade of the human visual system consisting of three links was described. 2D linear impulse response system 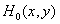 represents the optical elements of the eye. Link that performs elementwise non-linear transformation
represents the optical elements of the eye. Link that performs elementwise non-linear transformation 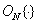 models the response of photoreceptors. Second two-dimensional impulse response system
models the response of photoreceptors. Second two-dimensional impulse response system 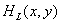 describes the process of lateral inhibition. The conversion performed by the entire modeling system is described by the expression
describes the process of lateral inhibition. The conversion performed by the entire modeling system is described by the expression
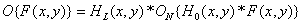 . (7.4.16)
. (7.4.16)
Mannos and Sakrison [2] carried out extensive measurements to develop a reliable rms criterion for the accuracy of single-color images based on the human visual system model. The effects in the optical system of the eye, leading to a deterioration in its resolution, were not taken into account, and the ratio (7.4.16) resulted in a simpler form:
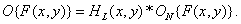 (7.4.17)
(7.4.17)
In these experiments, the original intensity distribution, which describes the original image, was subjected to element-wise nonlinear transformation according to a power or logarithmic law, and then spatial filtering with frequency response
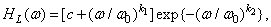 (7.4.18)
(7.4.18)
Where 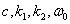 - permanent. Further, distortions were introduced into the obtained image, equivalent to those arising in the process of optimal coding with a given average number of binary digits per image element. Then the distorted image was subjected to inverse spatial filtering with frequency response.
- permanent. Further, distortions were introduced into the obtained image, equivalent to those arising in the process of optimal coding with a given average number of binary digits per image element. Then the distorted image was subjected to inverse spatial filtering with frequency response. 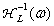 and inverse elementwise nonlinear transformation. The result was a distorted image in the form of an intensity distribution. All these operations were performed on a discrete image. A similar procedure was repeated for different images for different values of the average number of binary digits and other parameters. The quality of the obtained images was evaluated subjectively on a seven-point scale of the place in the group (Table 7.1.2) and ranking. It turned out that with the same average number of binary digits per element, the highest marks and places in the group were obtained by those images that were subjected to a filter with a frequency response shown in Fig. 7.4.1. In addition, a non-linear power-law transformation with an exponent of 1/3 gave much better results than a logarithmic transformation. Studies of Mannos and Sakrison also showed that the preliminary processing according to equality (7.4.17), performed before the image coding, creates more favorable conditions for coding. The results of these studies also certify the usefulness of the application of the RMS criterion of fidelity with the metric of the “geodesic space” characteristic of human vision. For quantitative study of this criterion of fidelity further research is needed.
and inverse elementwise nonlinear transformation. The result was a distorted image in the form of an intensity distribution. All these operations were performed on a discrete image. A similar procedure was repeated for different images for different values of the average number of binary digits and other parameters. The quality of the obtained images was evaluated subjectively on a seven-point scale of the place in the group (Table 7.1.2) and ranking. It turned out that with the same average number of binary digits per element, the highest marks and places in the group were obtained by those images that were subjected to a filter with a frequency response shown in Fig. 7.4.1. In addition, a non-linear power-law transformation with an exponent of 1/3 gave much better results than a logarithmic transformation. Studies of Mannos and Sakrison also showed that the preliminary processing according to equality (7.4.17), performed before the image coding, creates more favorable conditions for coding. The results of these studies also certify the usefulness of the application of the RMS criterion of fidelity with the metric of the “geodesic space” characteristic of human vision. For quantitative study of this criterion of fidelity further research is needed.
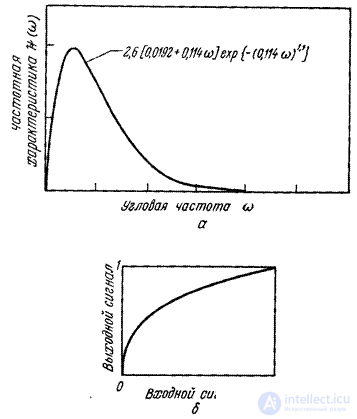
Fig. 7.4.1. Specifications 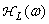 and
and  , providing the best subjective image quality when modeling the coding process [2]: a - frequency response; b - the characteristic of elementwise nonlinear transformation.
, providing the best subjective image quality when modeling the coding process [2]: a - frequency response; b - the characteristic of elementwise nonlinear transformation.
In systems of digital image processing to determine fidelity playback is usually much more convenient to use discrete samples, rather than analog images. Therefore, it is important to find fidelity criteria based on discrete readings that are in good agreement with the results of subjective assessments of continuous images.
The direct way to obtain such fidelity criteria is to simply “digitize” the corresponding analog criteria. For example, the normalized root mean square error (NSCO) describing the difference between the readings 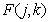 continuous reference image
continuous reference image 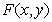 and counts
and counts 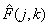 continuous distorted image
continuous distorted image 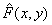 can be represented as
can be represented as
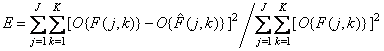 . (7.4.19)
. (7.4.19)
It can be shown that this measure coincides with the corresponding “continuous” measure described by relation (7.4.11) if the Nyquist criterion is satisfied when both images are sampled. Unfortunately, in real image processing systems, the readings based on which the reproduced continuous image is created are not its Nyquist counts, since the reproducing device introduces its own distortions and it is difficult to perform an optimal two-dimensional interpolation. However, the need often forces the use of features similar to (7.4.19), even in cases where they are inaccurate.
In tab. 7.4.1 some of the most common criteria of fidelity are shown, based on estimates of standardized mean square errors (NECS) for discrete images. Another widely used criterion of fidelity is the so-called peak mean square error (PSC), determined by
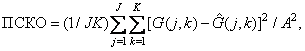 (7.4.20)
(7.4.20)
Where 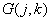 - the converted image corresponding to the definition given in table. 7.4.1, and the number
- the converted image corresponding to the definition given in table. 7.4.1, and the number 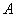 равно максимальному значению
равно максимальному значению 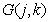 . Среднеквадратические ошибки часто измеряют в децибелах и рассматривают как отношение сигнал/шум (С/Ш):
. Среднеквадратические ошибки часто измеряют в децибелах и рассматривают как отношение сигнал/шум (С/Ш):
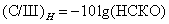 (7.4.21a)
(7.4.21a)
or
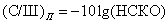 (7.4.21б)
(7.4.21б)
Таблица 7.4.1. Критерии верности, основанные на оценках нормированных среднеквадратических ошибок, для дискретных одноцветных изображений
Без преобразования
|
С поэлементным преобразованием
|
Степенной закон
|
Логарифмический закон
|
С преобразованием Лапласа Where
|
С использованием свертки
Where
|
Имея дело с операторами пространственных преобразований, такими, как оператор Лапласа или оператор свертки (табл. 7.4.1), не следует забывать, что массивы отсчетов изображений имеют конечные размеры. Поэтому пределы суммирования [в выражениях, подобных (7.4.19) или (7.4.20)] необходимо ограничивать центральными областями массивов 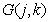 and
and 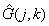 in order to avoid edge effects that appear when approximating continuous convolution integrals by discrete sums. These issues are discussed in more detail in chap. eleven.
in order to avoid edge effects that appear when approximating continuous convolution integrals by discrete sums. These issues are discussed in more detail in chap. eleven.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing