5.3. VECTOR REPRESENTATION OF IMAGES

In ch. 1 brightness, color coordinate, or some other suitable parameter describing the image, seemed to be a continuous function 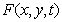. With the help of image sampling methods, discussed in Ch. 4, a continuous image recorded at some point in time can be represented as an array of samples 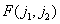in some rectangular area 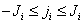. Often it is useful to consider this array as a matrix with 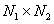elements:

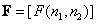, (5.3.1)

Where 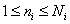, and the indices of counts are renumbered as is customary in the theory of matrices.

To facilitate the analysis, it is convenient to go from the matrix representation of the image to the vector one, collecting the elements of the columns (or rows) of the matrix 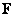in one long vector [9]. Formally, this operation can be represented by an auxiliary vector. 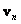size 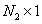and matrices 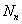defined as follows:

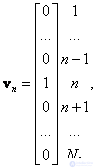
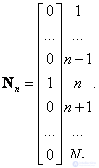(5.3.2)

In this case, the matrix 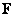will be presented in vector form using the ordering operation

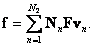(5.3.3)

Vector 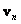highlights 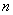matrix column 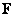and matrix 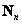puts this column in the space reserved for 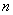of the vector segment 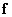. So the vector 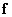contains all matrix elements 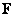consecutively read in columns. Inverse vector transform operation 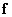to matrix 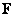described by the ratio

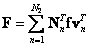. (5.3.4)

Using formulas (5.3.3) and (5.3.4), it is easy to establish a connection between the matrix and vector representations of a two-dimensional array. The advantages of representing the image in a vector form are the greater compactness of the notation and the possibility of directly using the methods developed for processing one-dimensional signals. It should be noted that expressions (5.3.3) and (5.3.4) not only describe the lexicographic connection between the matrix and the vector, but also define some operators that can be used in mathematical analysis. The following sections provide numerous examples of the use of these ordering operators.