Lecture
In linear signal processing, the problem of “inversion” of the transformation is often encountered.
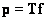 (8.3.1)
(8.3.1)
in order to express the exact value of the input vector 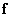 size
size 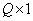 or some appreciation
or some appreciation 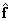 through the output vector p size
through the output vector p size 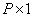 . If a
. If a 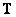 - square matrix, it is obvious that
- square matrix, it is obvious that
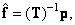 (8.3.2)
(8.3.2)
if the inverse matrix exists. If the matrix 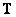 not square, then a pseudo-inverse matrix can be used to find the solution
not square, then a pseudo-inverse matrix can be used to find the solution 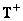 size
size 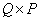 . In this case
. In this case
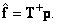 (8.3.3)
(8.3.3)
If the solution exists and is unique, then the “correct” pseudo-reversal operator will be the one that provides an exact estimate, i.e. 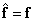 . This means that the vector
. This means that the vector 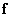 can be determined by the observed vector
can be determined by the observed vector 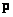 no mistakes. If a solution exists, but it is not unique, then using a pseudo-inverse operator, you can choose a solution with the minimum norm. If, finally, exact solutions do not exist, then using the pseudo-inversion operator one can find the best approximate solution. This issue is discussed in more detail in subsequent sections. Clarifications and proofs of many of the provisions below are contained in monographs [4-6].
no mistakes. If a solution exists, but it is not unique, then using a pseudo-inverse operator, you can choose a solution with the minimum norm. If, finally, exact solutions do not exist, then using the pseudo-inversion operator one can find the best approximate solution. This issue is discussed in more detail in subsequent sections. Clarifications and proofs of many of the provisions below are contained in monographs [4-6].
The first of the pseudo-inversion operators will be considered an operator with a generalized inverse matrix 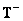 for which the following relations hold:
for which the following relations hold:
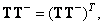 (8.3.4a)
(8.3.4a)
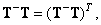 (8.3.46)
(8.3.46)
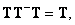 (8.3.4в)
(8.3.4в)
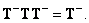 (8.3.4g)
(8.3.4g)
The generalized inverse matrix is unique and under certain conditions it can be written explicitly. If a 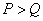 , then the system of equations (8.3.1) is called overdetermined, that is, the number of components of the observed vector
, then the system of equations (8.3.1) is called overdetermined, that is, the number of components of the observed vector 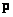 exceeds the number of vector components to be assessed
exceeds the number of vector components to be assessed 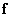 . If at the same time the rank of the matrix
. If at the same time the rank of the matrix 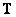 equals
equals 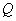 , then the generalized inverse matrix
, then the generalized inverse matrix
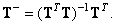 (8.3.5)
(8.3.5)
In the opposite case, when 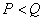 , system (8.3.1) is called underdetermined. If at the same time the rank of the matrix
, system (8.3.1) is called underdetermined. If at the same time the rank of the matrix 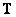 equals
equals 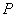 , then the generalized inverse matrix has the form
, then the generalized inverse matrix has the form
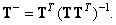 (8.3.6)
(8.3.6)
It is easy to show that the matrices defined by relations (8.3.5) and (8.3.6) satisfy conditions (8.3.4). If the matrix 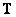 can be represented as a direct product (8.1.8), then the generalized inverse matrix has the form
can be represented as a direct product (8.1.8), then the generalized inverse matrix has the form
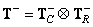 (8.3.7)
(8.3.7)
Where 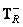 and
and 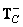 - generalized inverse matrices for linear row and column processing operators. In this case, the amount of computation required for conversion is reduced.
- generalized inverse matrices for linear row and column processing operators. In this case, the amount of computation required for conversion is reduced.
Another type of pseudo-reversal operator has a matrix 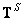 , called the least squares inversion matrix, which is defined by the following relations:
, called the least squares inversion matrix, which is defined by the following relations:
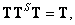 (8.3.8a)
(8.3.8a)
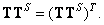 (8.3.8b)
(8.3.8b)
Finally, conditionally the inverse matrix 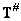 determined by the formula
determined by the formula
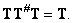 (8.3.9)
(8.3.9)
An analysis of the definitions of all three types of pseudo-inversion operators shows that the generalized inverse operator is the least-squares inversion operator, and the latter is the conditional inversion operator. For any linear operator with a matrix 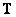 there is always a least squares inversion matrix and a conditionally inverse matrix, but they may not be the only ones. In addition, for these matrices it is usually not possible to find an explicit expression in a finite form.
there is always a least squares inversion matrix and a conditionally inverse matrix, but they may not be the only ones. In addition, for these matrices it is usually not possible to find an explicit expression in a finite form.
Below are some useful relationships for the matrix. 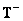 which is a generalized inverse matrix with respect to the matrix
which is a generalized inverse matrix with respect to the matrix 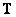 size
size 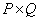 .
.
Generalized inversion of the transposed matrix
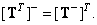 (8.3.10)
(8.3.10)
Generalized inversion of a generalized inverse matrix
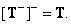 (8.3.11)
(8.3.11)
Saving rank
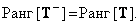 (8/3/12)
(8/3/12)
Generalized matrix matrix
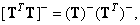 (8.3.13)
(8.3.13)
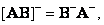 (8.3.14)
(8.3.14)
Where 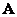 and
and 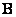 - rank matrices
- rank matrices 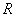 measuring
measuring 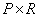 and
and 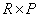 respectively.
respectively.
Generalized inversion of the product of orthogonal matrices
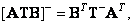 (8.3.15)
(8.3.15)
Where 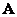 and
and 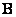 - orthogonal size matrices
- orthogonal size matrices 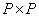 and
and 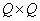 respectively.
respectively.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing