Content
- Introduction
- Property 1. Linearity
- Property 2. The time shift
- Property 3. DFT cyclic convolution of signals
- Property 4. Spectrum of the product of two signals
- Property 5. Frequency Shift Property
- Property 6. Inversion of the spectrum of a valid signal
- Duality property
- findings
Introduction
Previously, expressions for the direct and inverse discrete Fourier transforms were obtained. We give them again:
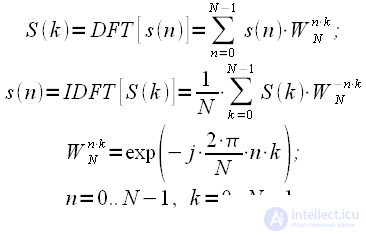 |
(one) |
Where
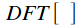
- DFT operator, and
- operator of the inverse DFT. Everywhere later in this article it is believed that
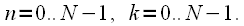
In this article we will consider the properties of the DFT.
Property 1. Linearity
The spectrum of the sum of the signals is equal to the sum of the spectra of these signals. If a
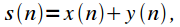
then the spectrum
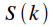
equals:
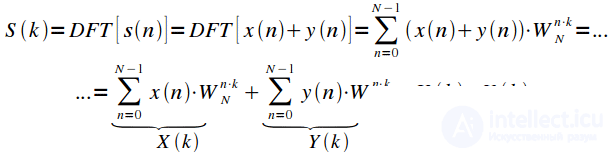 |
(2) |
Where
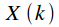
and
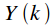
- signal spectra
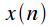
and
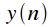
respectively.
When a signal is multiplied by a constant, the signal spectrum is also multiplied by a constant:
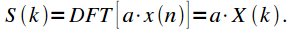 |
(3) |
Property 2. The time shift
Let the signal
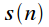
has a spectrum

. If you shift the signal
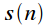
cyclically on
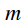
counts, i.e.
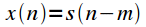
, then the spectrum of the shifted signal is equal to:
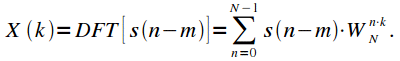 |
(four) |
Introduce variable substitution
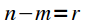
then
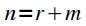
and expression (4) can be rewritten:
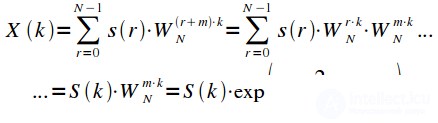 |
(five) |
Thus the cyclic shift of the signal by
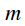
leads to a rotation of the phase spectrum, and the amplitude spectrum does not change.
Need to make a comment. Expression (5) is valid only for cyclic shift. An example of a cyclic shift is shown in Figure 1.
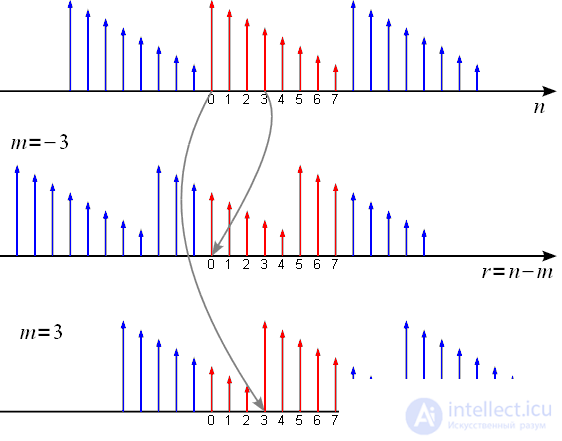
Figure 1: Example of a cyclic shift signal
The source signal is shown in red in the upper graph.
on average
with a shift
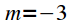
countdown (ahead), and in the lower graph
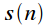
shifted by
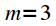
countdown (with delay). It can be seen that with cyclic shift when advancing the first
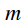
reports are transferred from the beginning to the end of the sample, and when they are late, the last
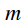
reports are transferred from the end of the sample to the beginning.
Property 3. DFT cyclic convolution of signals
Let the signal
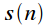
is the result of cyclical convolution of signals
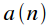
and
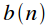
:
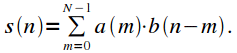 |
(6) |
Calculate the spectrum of the signal
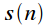
:
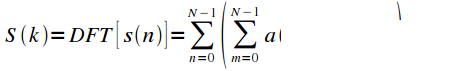 |
(7) |
Swap the summation operations:
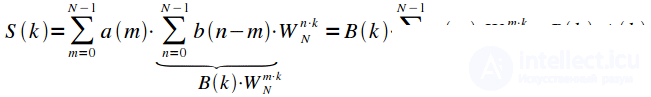 |
(eight) |
In deriving expression (8), the time shift property was used. Thus, it can be concluded that the spectrum of cyclical convolution of two signals is equal to the product of the spectra of these signals. This property allows you to use fast DFT algorithms to calculate convolution.
Property 4. Spectrum of the product of two signals
Let the signal
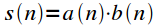
equal to the product of signals
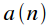
and
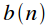
, and
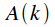
and
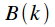
- signal spectra
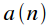
and
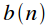
respectively.
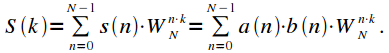 |
(9) |
Substitute in the expression (9) the expression for the signal
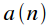
in the form of ODPP from the spectrum
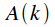
:
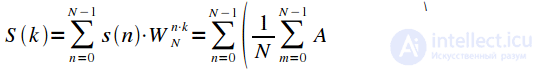 |
(ten) |
Swap the operations of summation in expression (10) and get:
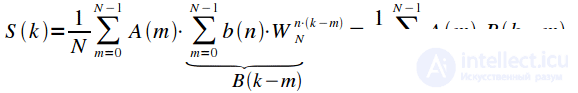 |
(eleven) |
Thus, the spectrum of the product of signals is a cyclical convolution of the spectra of these signals.
Property 5. Frequency Shift Property
Let the signal
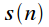
has a spectrum

. Perform a cyclic shift of the spectrum
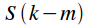
and consider the IDPF, then:
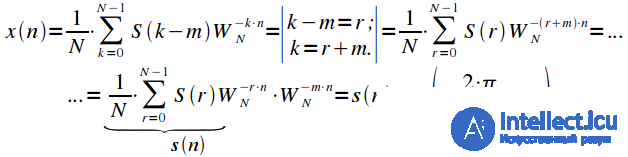 |
(12) |
Thus, we obtained that the shift of the spectrum is carried out by multiplying the signal by the complex exponent. It is important to note that after multiplying by a complex exponent, the signal will be complex, and its spectrum will cease to be symmetrical.
Property 6. Inversion of the spectrum of a valid signal
Inversion of the frequency spectrum of the actual signal is shown in Figure 2.
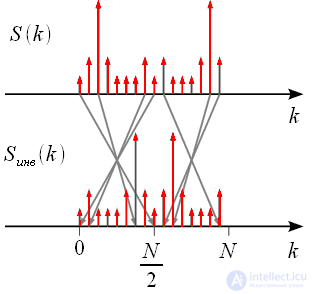
Figure 2: Inversion of the signal spectrum
If a
 -
- signal spectrum
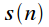
, the inverse spectrum
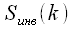
equals:
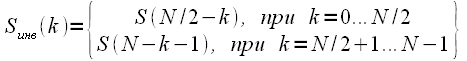 |
(13) |
Figure 3 shows that the spectrum inversion corresponds to a cyclic frequency shift of the spectrum by
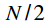
spectral counts in the direction of advance, or lag.
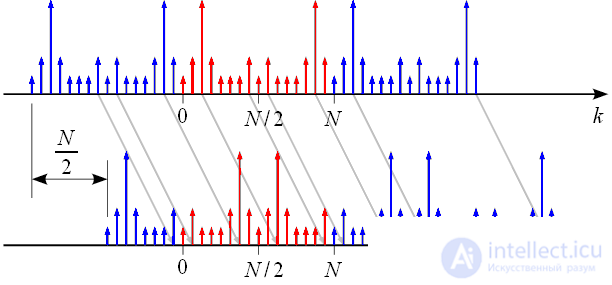
Figure 3: Inversion of the spectrum of the actual signal due to frequency shift
Then the signal with an inverse spectrum, according to (12) the property about the frequency shift of the spectrum is equal to:
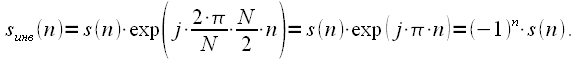 |
(14) |
Thus, to invert the spectrum of a signal, it is enough to multiply every second signal reading by minus one. In this case, multiplying by minus one even sample counts corresponds to a cyclic shift of the spectrum to the right by
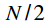
spectral samples, and multiplying odd samples corresponds to a cyclic shift of the spectrum to the left by
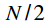
spectral counts.
Duality property
We considered the basic properties of the DFT. The DFT has one more remarkable property: the property of duality, which consists in the fact that all the properties of the DFT are valid both for the signal and for the spectrum. For example, we can consider property 3 of the DFT, which reads as follows: the spectrum of cyclical convolution of signals is the product of the spectra. At the same time, this can be stated in the opposite direction: the spectrum of the product of signals is the cyclic convolution of the spectra of these signals (property 4). Similarly, we can reformulate property 5 from property 3: a shift in time leads to a multiplication of the spectrum by a complex exponent, while multiplying a signal by a complex exponent leads to a cyclic shift of the spectrum. Using the property of duality, it can be assumed based on property 6, that multiplying every second spectral sample by minus one will invert the signal according to (13). Indeed, from Figure 3 it follows that the inversion according to (13) will be when the signal or spectrum is shifted by
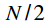
counts. In this case, from the expression (5) the signal spectrum with a cyclic shift on
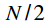
equals:
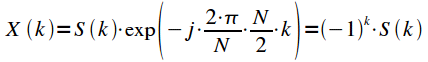 |
(15) |
We obtained that for the inversion of a signal in time, it is necessary to multiply every second sample of its spectrum by minus one, as we assumed using the DFT duality property.
findings
Thus, we considered the basic properties of the DFT: linearity, properties of the time and frequency shifts, the convolution spectrum and the product of the signals, and analyzed the spectrum and signal inversion. The duality of the DFT was also shown, which makes it possible to formulate properties simultaneously for both the spectrum and the signal.
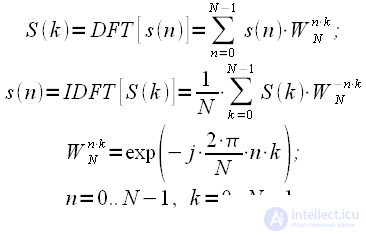
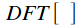 - DFT operator, and
- DFT operator, and 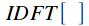 - operator of the inverse DFT. Everywhere later in this article it is believed that
- operator of the inverse DFT. Everywhere later in this article it is believed that 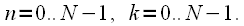
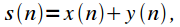 then the spectrum
then the spectrum 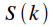 equals:
equals: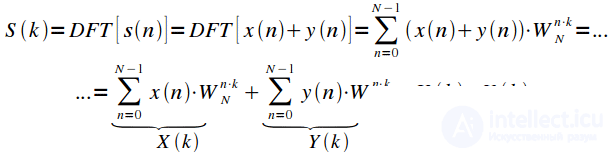
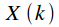 and
and 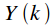 - signal spectra
- signal spectra 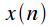 and
and 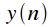 respectively.
respectively.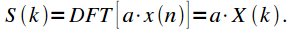
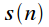 has a spectrum
has a spectrum  . If you shift the signal
. If you shift the signal 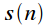 cyclically on
cyclically on 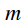 counts, i.e.
counts, i.e. 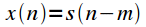 , then the spectrum of the shifted signal is equal to:
, then the spectrum of the shifted signal is equal to: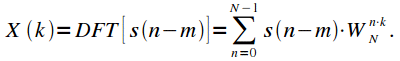
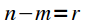 then
then 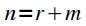 and expression (4) can be rewritten:
and expression (4) can be rewritten: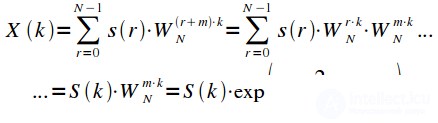
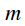 leads to a rotation of the phase spectrum, and the amplitude spectrum does not change.
leads to a rotation of the phase spectrum, and the amplitude spectrum does not change.
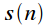 on average
on average 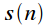 with a shift
with a shift 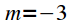 countdown (ahead), and in the lower graph
countdown (ahead), and in the lower graph 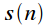 shifted by
shifted by 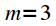 countdown (with delay). It can be seen that with cyclic shift when advancing the first
countdown (with delay). It can be seen that with cyclic shift when advancing the first 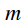 reports are transferred from the beginning to the end of the sample, and when they are late, the last
reports are transferred from the beginning to the end of the sample, and when they are late, the last 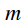 reports are transferred from the end of the sample to the beginning.
reports are transferred from the end of the sample to the beginning.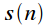 is the result of cyclical convolution of signals
is the result of cyclical convolution of signals 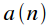 and
and 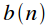 :
: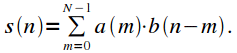
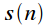 :
: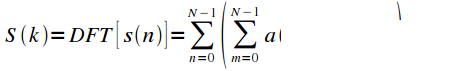
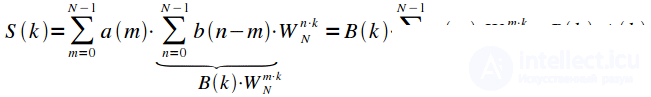
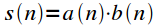 equal to the product of signals
equal to the product of signals 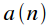 and
and 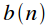 , and
, and 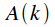 and
and 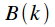 - signal spectra
- signal spectra 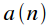 and
and 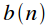 respectively.
respectively.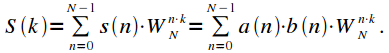
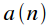 in the form of ODPP from the spectrum
in the form of ODPP from the spectrum 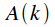 :
: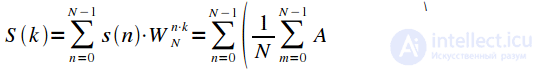
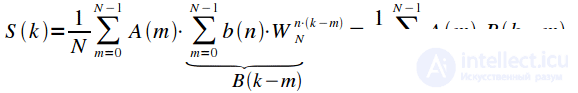
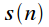 has a spectrum
has a spectrum  . Perform a cyclic shift of the spectrum
. Perform a cyclic shift of the spectrum 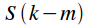 and consider the IDPF, then:
and consider the IDPF, then: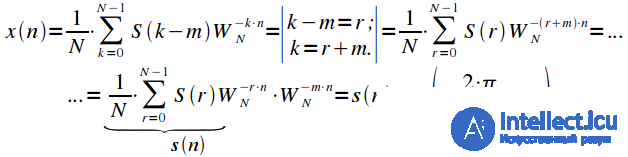

 - signal spectrum
- signal spectrum 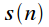 , the inverse spectrum
, the inverse spectrum 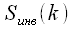 equals:
equals: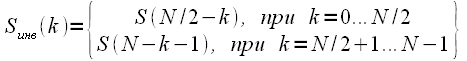
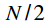 spectral counts in the direction of advance, or lag.
spectral counts in the direction of advance, or lag.
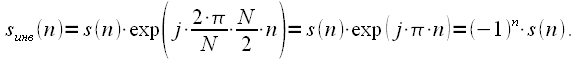
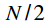 spectral samples, and multiplying odd samples corresponds to a cyclic shift of the spectrum to the left by
spectral samples, and multiplying odd samples corresponds to a cyclic shift of the spectrum to the left by 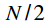 spectral counts.
spectral counts.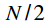 counts. In this case, from the expression (5) the signal spectrum with a cyclic shift on
counts. In this case, from the expression (5) the signal spectrum with a cyclic shift on 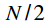 equals:
equals: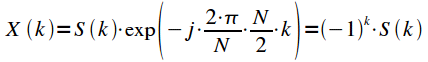
Comments
To leave a comment
Digital signal processing
Terms: Digital signal processing