Lecture
In general, in order to perform a unitary transformation of an image matrix containing 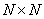 elements, and get the matrix from
elements, and get the matrix from 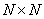 spectral coefficients, it is necessary to produce approximately
spectral coefficients, it is necessary to produce approximately 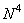 arithmetic operations (multiplications and additions). If the dimensions of the image matrix are large, then the number of operations becomes excessively large. Fortunately, for many unitary transformations, there are effective computational algorithms that make it possible to speed up the conversion.
arithmetic operations (multiplications and additions). If the dimensions of the image matrix are large, then the number of operations becomes excessively large. Fortunately, for many unitary transformations, there are effective computational algorithms that make it possible to speed up the conversion.
The main idea of these fast computational algorithms is the division of the whole task into a series of stages, and the results obtained at the previous stages are reused at the subsequent stages. As an example, consider the process of calculating the Hadamard transform coefficients with an unordered matrix for a sequence of four elements 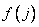 . With the direct method of calculation, four values are found using the formulas
. With the direct method of calculation, four values are found using the formulas
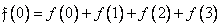 (10.10.1a)
(10.10.1a)
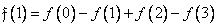 (10.10.1b)
(10.10.1b)
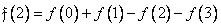 (10.10.1b)
(10.10.1b)
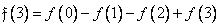 . (10.10.1g)
. (10.10.1g)
To do this, you must perform 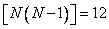 arithmetic operations (additions and subtractions). However, the Hadamard transform coefficients can be found differently by breaking up the calculation process into the following steps:
arithmetic operations (additions and subtractions). However, the Hadamard transform coefficients can be found differently by breaking up the calculation process into the following steps:
First stage
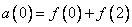 (10.10.2a)
(10.10.2a)
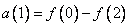 (10.10.2b)
(10.10.2b)
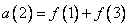 (10.10.2v)
(10.10.2v)
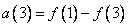 . (10.10.2g)
. (10.10.2g)
Second phase
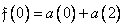 (10.10.3a)
(10.10.3a)
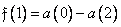 , 10.10.3b
, 10.10.3b
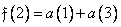 (10.10.4b)
(10.10.4b)
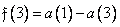 . (10.10.3g)
. (10.10.3g)
Moreover, to determine the elements of the matrix 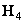 only required
only required 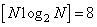 operations, i.e., four operations are saved.
operations, i.e., four operations are saved.
The course of the above calculations can be described using the graph (Fig. 10.10.1). The total number of operations is half the number of edges connecting the vertices of the graph. Another way of representing the same process is to factor the matrix when the Hadamard transform matrix 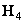 recorded as the product of two sparse matrices. For example,
recorded as the product of two sparse matrices. For example,
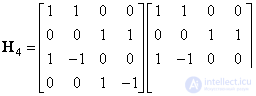 . (10.10.4)
. (10.10.4)
The number of operations is equal to half the number of nonzero elements in both matrix-factors.
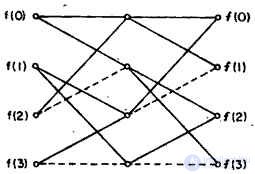
Fig. 10.10.1. Hadamard transform coefficient calculation graph for four-element sequence. (Solid lines denote addition operations, dashed lines represent subtractions.)
The principles described above using the Hadamard transform as an example can be applied to quickly calculate many other transformations. Fast algorithms have been developed for Fourier transforms [35], even cosine [12], sine [13], Hadamard [17], Haar [1] and oblique [26]. In the general case, no fast algorithm was found for the Karhunen-Loev transform, however, approximate Karhunen-Loeva transform algorithms for Markov processes are known.
For most one-dimensional unitary transformations, the order of the required number of arithmetic operations is equal to 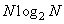 . The exception is the Haar transform, which has a sparse matrix and can therefore be calculated using approximately
. The exception is the Haar transform, which has a sparse matrix and can therefore be calculated using approximately 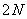 operations. For unitary transformations, the general method for constructing efficient computational algorithms is still unknown [36]. In each case, it is necessary to find an effective calculation procedure or a method for representing a matrix as a product of sparse matrices.
operations. For unitary transformations, the general method for constructing efficient computational algorithms is still unknown [36]. In each case, it is necessary to find an effective calculation procedure or a method for representing a matrix as a product of sparse matrices.
Unitary transformations based on sine-wave basis vectors (Fourier transform, cosine, sine) can be performed indirectly using the so-called 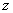 -transformations with chirp filtering. Fourier transform of one-dimensional sequence
-transformations with chirp filtering. Fourier transform of one-dimensional sequence 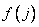 determined by the ratio
determined by the ratio
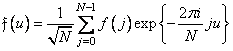 . (10.10.5).
. (10.10.5).
Replacing variables
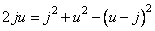 (10.10.6)
(10.10.6)
can get expression
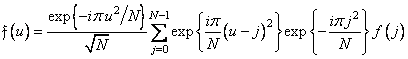 . (10.10.7)
. (10.10.7)
Formula (10.10.7) describes the combination of the following operations:
1. Element multiplication sequence 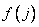 factor with quadratically variable phase
factor with quadratically variable phase 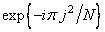 .
.
2. Convolution of the results of the previous operation with the core 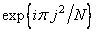 .
.
3. The element-wise multiplication of the resulting sequence by factors with a quadratic phase 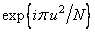 .
.
In fig. 10.10.2 shows a block diagram of the algorithm for calculating the Fourier transform coefficients using the method 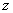 -transformations with chirp filtering. If the processing is performed in a universal digital computer, then, as a rule, this algorithm should not be used, since a larger number of operations are required to calculate the convolution than to directly perform the FFT transformation. However, using analog transversal filters is very easy to implement.
-transformations with chirp filtering. If the processing is performed in a universal digital computer, then, as a rule, this algorithm should not be used, since a larger number of operations are required to calculate the convolution than to directly perform the FFT transformation. However, using analog transversal filters is very easy to implement. 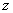 -transformation with chirp filtering, which makes it possible to calculate the Fourier transform coefficients, as well as the cosine and sine transforms in a continuous way.
-transformation with chirp filtering, which makes it possible to calculate the Fourier transform coefficients, as well as the cosine and sine transforms in a continuous way.
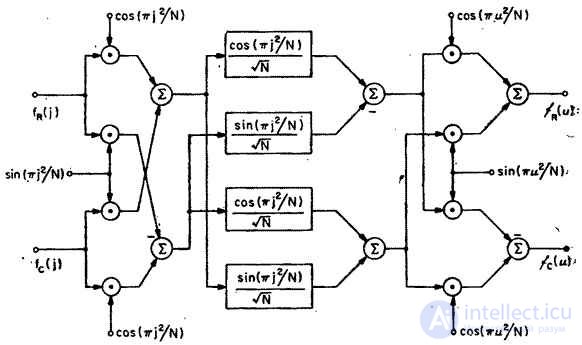
Fig. 10.10.2. A block diagram of the Fourier transform algorithm using the method 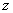 -conversion.
-conversion.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing