10.8. TRANSFORMATION OF KARUNEN-LOEVA

The method of converting continuous signals into a set of uncorrelated coefficients was developed by Karhunen [27] and Loeev [28]. As indicated in [30], Hotelling [29] first proposed a method for converting discrete signals into a set of uncorrelated coefficients. However, in most works on digital signal processing, both discrete and continuous transformations are called the Karhunen-Loeve transform or decomposition into eigenvectors.

In the general case, the Karhunen-Loeva transform is described by the relation

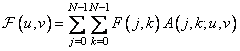(10.8.1)

core 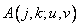which satisfies the equation

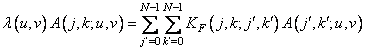(10.8.2)

Where 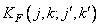- the covariance function of the sampled image, and 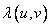with fixe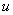d and 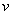is constant. Functions 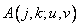are eigenfunctions of the covariance function, and 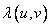- her own values. As a rule, it is not possible to express eigenfunctions explicitly.

If the covariance function can be divided, i.e.

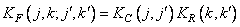(10.8.3)

then the Karunen-Loeva decomposition core is also separable and

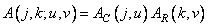. (10.8.4)

The rows and columns of the matrices describing these kernels satisfy the following equations:

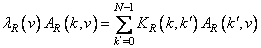, (10.8.5)

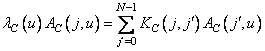. (10.8.6)

In the particular case when the covariance matrix describes a first-order separable Markov process, it is possible to write eigenfunctions in explicit form. For a one-dimensional Markov process with a correlation coefficient 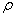Eigenfunctions and eigenvalues ​​have the form [3]

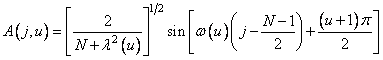(10.8.7)

and

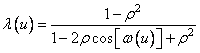, (10.8.8)

Where 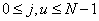a 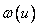- roots of the transcendental equation

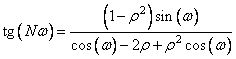. (10.8.9)

The eigenvectors can also be found from the recurrence formulas [32]

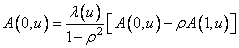, (10.8.10a)

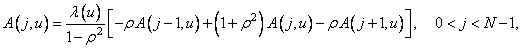(10.8.10b)

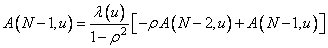, (10.8.10b)

putting as initial condition 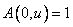and then normalizing the resulting eigenvectors.

If the original and transformed images are presented in vector form, then a pair of Karhunen-Loeve transformations will have the form

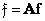(10.8.11)

and

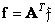. (10.8.12)

Transformation matrix 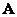satisfies the equation

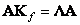(10.8.13)

Where - vector covariance matrix 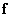; 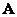- matrix whose rows are eigenvectors of the matrix ; 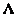- diagonal matrix of the form

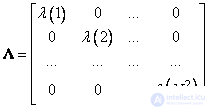. (10.8.14)

If the matrix separable then

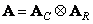(10.8.15)

and matrix 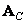and 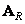satisfy the following conditions:

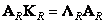(10.8.16a)

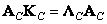(10.8.16b)

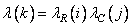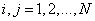but at [33].

In fig. 10.8.1 shows the graphs of basis functions of the Karhunen-Loeve transform of a one-dimensional Markov process, for which the correlation coefficients of neighboring elements .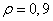

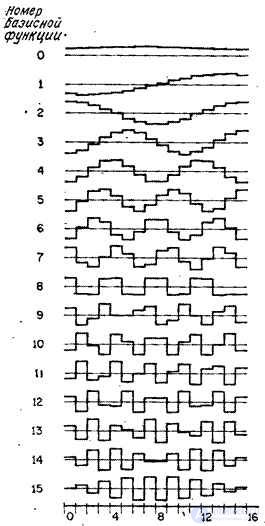
Fig. 10.8.1. The basic functions of the transformation of the Karunen-Loeva with .