Lecture
Consider an array 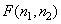 of
of 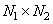 elements representing the source (input) image. When exposed to it by a generalized linear operator, an array is obtained from
elements representing the source (input) image. When exposed to it by a generalized linear operator, an array is obtained from 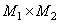 elements describing the transformed (output) image
elements describing the transformed (output) image
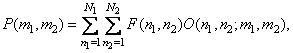 (8.1.1)
(8.1.1)
where is the core operator 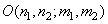 is a set of weighting factors that, in general, depend on the coordinates of elements of both the input and output images.
is a set of weighting factors that, in general, depend on the coordinates of elements of both the input and output images.
When analyzing linear image processing operations, it is convenient to use the vector representations described in Ch. 5 [1]. Therefore, we assume that the input array 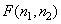 presented or as a matrix
presented or as a matrix 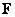 or as a vector
or as a vector 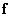 obtained by scanning the matrix
obtained by scanning the matrix 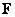 by columns. Similarly, assume that the output array
by columns. Similarly, assume that the output array 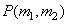 can be represented by either a matrix
can be represented by either a matrix 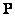 or in the form of its sweep by columns, i.e. by vector
or in the form of its sweep by columns, i.e. by vector 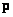 . To simplify the notation, it will be assumed below that the matrices representing the input and output images are square with dimensions
. To simplify the notation, it will be assumed below that the matrices representing the input and output images are square with dimensions 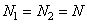
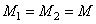 respectively. Now suppose that the symbol
respectively. Now suppose that the symbol 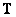 denotes a size matrix
denotes a size matrix  with which the vector of the original image
with which the vector of the original image 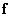 size
size 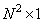 linearly converted to vector
linearly converted to vector
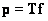 (8.1.2)
(8.1.2)
output image size. The matrix 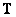 can be divided into blocks - matrix
can be divided into blocks - matrix 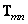 size
size 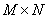 (the number of which is also equal to
(the number of which is also equal to 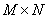 ) - and present it as follows:
) - and present it as follows:
 (8.1.3)
(8.1.3)
In accordance with the relation (5.3.3), the output image vector 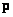 can be expressed through the input image matrix
can be expressed through the input image matrix 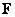 :
:
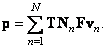 (8.1.4)
(8.1.4)
In addition, using equality (5.3.4), the matrix 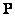 output image can be expressed through the vector p of the same image:
output image can be expressed through the vector p of the same image:
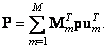 (8.1.5)
(8.1.5)
From these formulas, we obtain an expression connecting the input and output matrices:
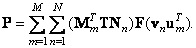 (8.1.6)
(8.1.6)
Note that the operators 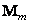 and
and 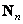 just isolated from the matrix
just isolated from the matrix 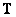 block
block 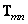 . Consequently,
. Consequently,
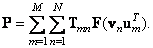 (8.1.7)
(8.1.7)
Let the linear transformation be separable, i.e. the matrix 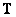 can be represented as a direct work
can be represented as a direct work
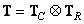 (8.1.8)
(8.1.8)
Where 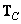 and
and 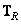 - operators to convert columns and rows of the image matrix
- operators to convert columns and rows of the image matrix 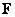 . In this case
. In this case
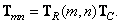 (8.1.9)
(8.1.9)
Consequently,
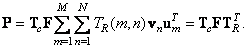 (8.1.10)
(8.1.10)
Thus, the output image matrix 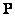 can be obtained by sequential processing of the matrix
can be obtained by sequential processing of the matrix 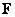 by rows and columns.
by rows and columns.
When processing images in many cases, it turns out that the linear transformation operator 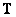 has a specific structure that allows to simplify computational operations. The following are important special cases illustrated in Fig. 8.1.1, when the dimensions of the input and output images are the same, i.e.
has a specific structure that allows to simplify computational operations. The following are important special cases illustrated in Fig. 8.1.1, when the dimensions of the input and output images are the same, i.e. 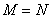 .
.
a) When processing the matrix 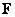 column only
column only
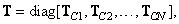 (8.1.11)
(8.1.11)
Where 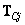 - conversion matrix for
- conversion matrix for 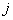 th column.
th column.
b) With the same processing of each column of the matrix 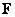
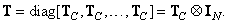 (8.1.12)
(8.1.12)
c) When processing the matrix 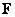 only in rows
only in rows
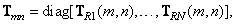 (8.1.13)
(8.1.13)
Where 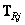 - conversion matrix for
- conversion matrix for 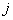 line
line
d) With the same processing of each row of the matrix 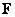
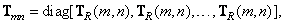 (8.1.14a)
(8.1.14a)
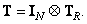 (8.1.14b)
(8.1.14b)
e) With the same processing of columns and the same processing of rows of the matrix 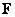
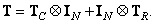 (8.1.15)
(8.1.15)
The number of arithmetic operations performed in each of these cases is shown in Table. 8.1.1.
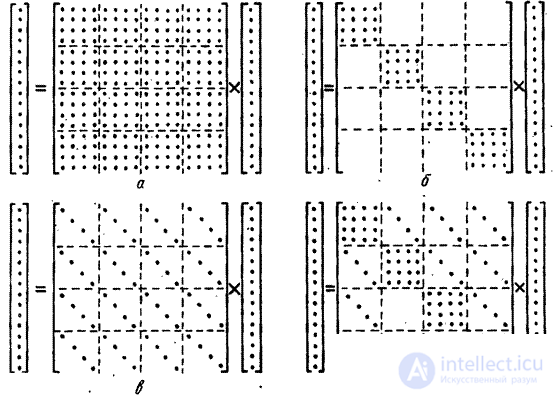
Fig. 8.1.1. The matrix structure of a linear operator: a - the general case; b - processing only by columns; in - processing only lines; d - processing only rows and columns.
Table 8.1.1. The number of arithmetic operations for linear transformation
Happening | Number of multiplications and additions |
Overall Column Processing Row processing Processing rows and columns Processing with a splittable matrix |
|
From relation (8.1.10) it can be seen that if a two-dimensional linear transformation has a separable matrix, then it can be performed by sequential one-dimensional processing of rows and columns of the sample array. As follows from the table. 8.1.1, for such transformations it is possible to significantly reduce the number of required computational operations: in the general case, when calculating by the formula (8.1.2), 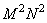 operations, but if you can use the formula (8.1.10), it is enough
operations, but if you can use the formula (8.1.10), it is enough 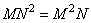 operations. Moreover, in this case the matrix
operations. Moreover, in this case the matrix 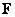 can be stored in a storage device (memory) with sequential access, for example, on a disk or on a drum, and read line by line, i.e. there is no need to store the matrix
can be stored in a storage device (memory) with sequential access, for example, on a disk or on a drum, and read line by line, i.e. there is no need to store the matrix 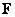 in a more expensive random access memory. It is necessary, however, to transpose the results of the transformations in columns in order to perform row-wise transformations. In the works [2, 3] algorithms are described for transposing matrices recorded in a memory with sequential access.
in a more expensive random access memory. It is necessary, however, to transpose the results of the transformations in columns in order to perform row-wise transformations. In the works [2, 3] algorithms are described for transposing matrices recorded in a memory with sequential access.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing