4.3.3. INFLUENCE OF IMMEDIATE RESTORING FILTERS

Let us now analyze the work of real systems for the recovery of continuous images. We will assume that the input signal of such a system consists of samples of some source image obtained at the Nyquist frequency using a finite set of delta functions. According to equality (4.1.9), the reconstructed image is described by the function

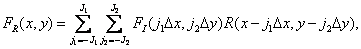(4.3.3)

Where 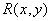- two-dimensional interpolation function. In the ideal case, the reconstructed image should be an exact copy of the original, i.e.

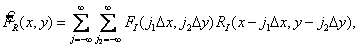(4.3.4)

Where denotes the optimal interpolation function, for example, given by formula (4.1.14) or (4.1.16). In this case, the recovery error for an arbitrary point of the image is equal to

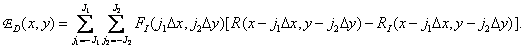(4.3.5)

The magnitude of the recovery error depends on two factors: a) in the real system, the interpolation function 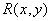may differ from the ideal interpolation function , b) the reconstructed image has finite dimensions and, therefore, the interpolation functions are cut off at its boundaries. In most systems operating with discretized images, recovery errors near the boundaries are usually neglected, since they become very small as the sample is removed from the image boundaries by several discretization steps. The non-ideality of interpolation functions in principle leads to a deterioration in the sharpness of the image, as well as to the appearance of parasitic high-frequency components.

It is convenient to investigate the effect of the non-ideality of the restoring filter considering the structure of the spectrum of the reconstructed image defined by the relation (4.1.11):

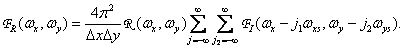(4.3.6)

Ideally, the multiplier 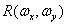should allocate components of the zero order spectrum at 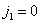, , 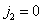and all other components must be suppressed. In a non-ideal filter, components of the zero-order spectrum can be weakened, which leads to a deterioration of sharpness, and, in addition, the harmonics of higher-order spectra can not be completely suppressed, which distorts the reconstructed image. In fig. 4.3.7 shows an example showing the nature of the distortion of the image when using a non-ideal recovery filter. A typical section of the sampled image spectrum is shown in Fig. 4.3.7, a. When using the ideal recovery filter, when the interpolation functions are 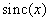, the components of the spectrum of zero order are highlighted, and all the components of the side spectra are completely suppressed (Fig. 4.3.7, c). In fig. 4.3.7, d shows the frequency response of a recovery filter based on a zero-order interpolation function, when the values ​​of the reconstructed elements in the vicinity of the reference point are set equal to the value at the reference point. The result is a spectrum (Fig. 4.3.7, d), distorted due to the weakening of some components of the spectrum of zero order and the appearance of spurious high-frequency components.

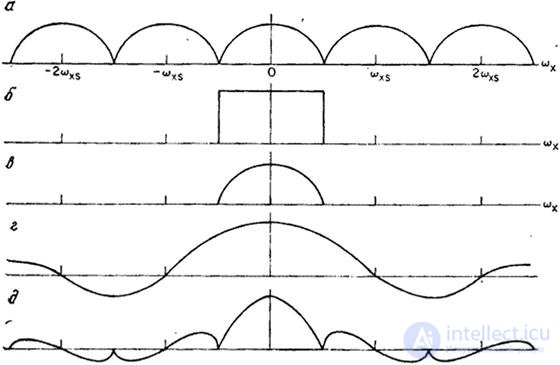
Fig. 4.3.7. Energy spectra with ideal and non-ideal reconstruction: a - sampled image spectrum; b - frequency response of an ideal recovery filter; in the spectrum of the image after the perfect recovery; g - frequency response of the recovery filter with interpolation of zero order; d - the spectrum of the image reconstructed with interpolation of zero order.

Repeating the steps taken in deriving equality (4.2.21), we find that the loss of sharpness caused by the imperfection of the restoring function 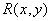, quantitatively can be expressed using the relationship

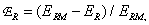(4.3.7)

where is the integral

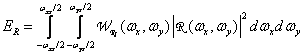(4.3.8)

represents the energy of those components of the imperfectly reconstructed image that lie in the Nyquist range, and the integral

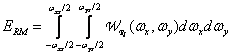(4.3.9)

describes the energy of such components of a perfectly reconstructed image.

Recovery error associated with the introduction of false high-frequency components of the spectrum can be determined by the ratio

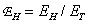(4.3.10)

Where

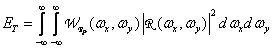(4.3.11)

there is the full energy of the reconstructed image, and

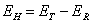(4.3.12)

represents the energy of all the spectral components of the reconstructed image lying outside the Nyquist range.

In tab. 4.3.2 shows recovery error values 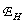and coefficient of loss of sharpness 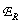obtained by reconstructing using some two-dimensional separable interpolation functions.

Table 4.3.2. Recovery error and loss of sharpness for various separable two-dimensional interpolation functions

Here it was assumed that the spectral density of the original image is described by the formulas

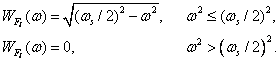(4.3.13)

In addition, it was assumed that the contribution made to the error in the recovery of the side spectra with 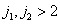, is negligible. The table shows that when restoring using rectangular interpolation functions (functions of zero order), the coefficient of loss of sharpness and the error of recovery are rather large. By using interpolation functions of a higher order, the recovery error can be significantly reduced, but at the expense of further deterioration in the coefficient of loss of sharpness