Lecture
It would be useful to know the probability density of the elements of the transformed image for an arbitrary transformation. Unfortunately, to find this density is not easy, as usually we do not have a complete description of the probability density of the original image. In addition, the transformations themselves are usually complex mathematical operations. However, the above transformations used for image processing are reduced to calculating the weighted sums of all elements of the original image. Therefore, using the central limit theorem of probability theory, we can conclude that the probability density of the elements of the transformed image is close to Gaussian with the moments that were found in the previous section.
The Fourier transform coefficients are complex numbers, and they can be specified using the real and imaginary parts or the module and argument. In both cases, each coefficient corresponds to two numbers that need to be quantized. We can assume that the real 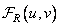 and imaginary
and imaginary 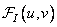 parts of the Fourier coefficient have the same Gaussian distributions, the dispersion of which
parts of the Fourier coefficient have the same Gaussian distributions, the dispersion of which 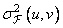 proportional to the energy spectrum of the original image. In this way,
proportional to the energy spectrum of the original image. In this way,
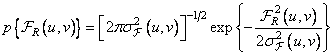 (10.12.1а)
(10.12.1а)
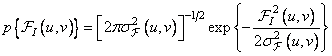 . (10.12.1b)
. (10.12.1b)
If the real and imaginary components have a Gaussian distribution, then the modulus of the Fourier coefficient 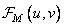 distributed according to the Rayleigh law. In this way,
distributed according to the Rayleigh law. In this way,
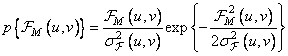 (10.12.2)
(10.12.2)
at 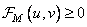 and phase
and phase 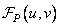 has a uniform distribution
has a uniform distribution
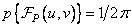 (10.12.3)
(10.12.3)
Where 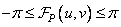 .
.
We can assume that the actual coefficients of other transformations have Gaussian distributions of the form
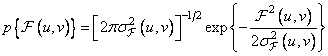 . (10.12.4)
. (10.12.4)
The density of the Rayleigh probability distribution (10.12.2) is often used as a model of the probability density of the constant component. 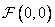 brightness images, since for such images the coefficient
brightness images, since for such images the coefficient 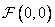 always strictly positive. The considered probability density models are widely used in the development of image conversion coding methods.
always strictly positive. The considered probability density models are widely used in the development of image conversion coding methods.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing