Lecture
We first consider the discrete superposition operator of a finite array of samples (for simplicity, it is assumed that all arrays of samples are square) 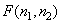 (Where
(Where 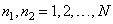 ) with finite array
) with finite array 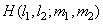 (Where
(Where 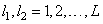 ), playing the role of impulse response. In the general case, the impulse response may vary depending on the coordinates
), playing the role of impulse response. In the general case, the impulse response may vary depending on the coordinates 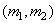 readout in the output array
readout in the output array  . The operation of superposition in a limited area is determined by the ratio
. The operation of superposition in a limited area is determined by the ratio
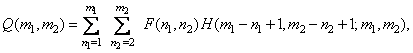 (9.1.1)
(9.1.1)
Where 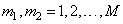 and arrays
and arrays 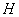 and
and 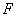 have zero values outside the ranges of the corresponding indices. Analyzing the limiting values of the indices of the impulse response counts, we can be sure that
have zero values outside the ranges of the corresponding indices. Analyzing the limiting values of the indices of the impulse response counts, we can be sure that 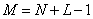 and therefore the output array
and therefore the output array 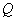 It is larger than the original (Fig. 9.1.1).
It is larger than the original (Fig. 9.1.1).
If arrays 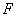 and
and 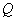 presented respectively as a vector
presented respectively as a vector 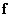 size
size 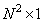 and vectors
and vectors 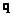 size
size 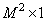 , then the transform (9.1.1) can be written as [1]
, then the transform (9.1.1) can be written as [1]
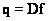 , (9.1.2)
, (9.1.2)
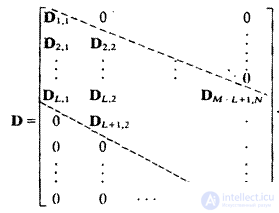
Where 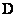 - size matrix
- size matrix 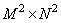 containing impulse response counts. The matrix
containing impulse response counts. The matrix 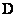 superposition operator conveniently divided into blocks
superposition operator conveniently divided into blocks 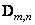 size
size 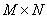 .
.
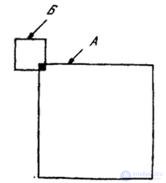
Fig. 9.1.1. The superposition of the final arrays of the impulse response samples and the original image: A - passive from 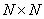 image readouts; B - rotated 180 ° array of
image readouts; B - rotated 180 ° array of 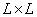 impulse response counts.
impulse response counts.
Analyzing the limits of summation in expression (9.1.1), it can be shown that
 (9.1.3)
(9.1.3)
Arbitrary nonzero matrix element 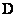 has the appearance
has the appearance
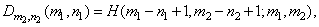 (9.1.4)
(9.1.4)
Where 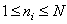 , but
, but 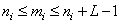 . It follows that the matrix
. It follows that the matrix 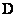 It has a regular structure and is rather rarely filled, with nonzero blocks grouped as a band in the middle part of the matrix.
It has a regular structure and is rather rarely filled, with nonzero blocks grouped as a band in the middle part of the matrix. 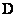 , contain zones of zero elements.
, contain zones of zero elements.
If the form of the impulse response is invariant with respect to the shift (that is, the same for all points of the output array), then the structure of the matrix 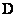 independent of coordinates
independent of coordinates 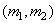 output countdown. Then
output countdown. Then
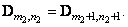 (9.1.5)
(9.1.5)
Thus, all columns of the matrix 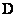 formed by shifting the first column. In this case, the superposition operator is called the convolution operator of finite arrays. In fig. 9.1.2; a shows the printouts of matrices obtained in the convolution of final arrays obtained on the digital computer, for the case when the input array has dimensions
formed by shifting the first column. In this case, the superposition operator is called the convolution operator of finite arrays. In fig. 9.1.2; a shows the printouts of matrices obtained in the convolution of final arrays obtained on the digital computer, for the case when the input array has dimensions 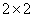 (
( 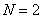 ) output array
) output array 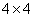 (
( 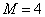 ), and an array of impulse response counts
), and an array of impulse response counts 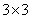 (
( 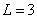 ). Pairs of integers
). Pairs of integers 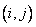 in the matrix
in the matrix 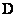 designate
designate 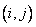 matrix element
matrix element 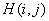 .
.

Fig. 9.1.2. Examples of matrices of convolution operators of finite arrays: a - the general case, 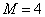 ,
, 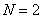 ,
, 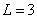 ; b - impulse response of the Gaussian form,
; b - impulse response of the Gaussian form, 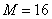 ,
, 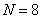 ,
, 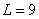 .
.
Matrix structure 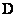 is better seen in the example of the larger matrix shown in Fig. 9.1.2, b. In the matrix
is better seen in the example of the larger matrix shown in Fig. 9.1.2, b. In the matrix 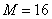 ,
, 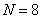 ,
, 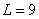 , and the impulse response is symmetric and has a Gaussian form. Note that in this example, the dimensions of the matrix
, and the impulse response is symmetric and has a Gaussian form. Note that in this example, the dimensions of the matrix  equal to 256
equal to 256  64.
64.
Using the technique applied in deriving the relation (8.1.7), the superposition operator can be represented in the matrix form
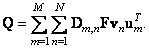 (9.1.6)
(9.1.6)
If the impulse response is shift-invariant and separable, i.e.
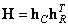 , (9.1.7)
, (9.1.7)
Where 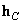 and
and 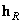 - the column vector, describing, respectively, the nature of the change of the impulse response in columns and rows, then
- the column vector, describing, respectively, the nature of the change of the impulse response in columns and rows, then
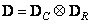 . (9.1.8)
. (9.1.8)
Matrices 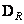 and
and 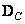 have dimensions
have dimensions 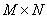 and species structure
and species structure
 . (9.1.9)
. (9.1.9)
The operation of two-dimensional convolution in this case is reduced to the sequential calculation of one-dimensional convolutions in rows and columns. In this way,
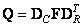 . (9.1.10)
. (9.1.10)
To obtain the final convolution or superposition, in general, you must perform 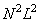 arithmetic operations, and this number does not include multiplication by zero elements of the matrix
arithmetic operations, and this number does not include multiplication by zero elements of the matrix 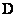 . If the operator is separable, that is, it satisfies equality (9.1.10), then it suffices to execute
. If the operator is separable, that is, it satisfies equality (9.1.10), then it suffices to execute 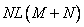 operations.
operations.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing