8.4. SOLUTION OF SYSTEMS OF LINEAR EQUATIONS

Linear equation system

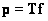(8.4.1)

Where 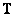- size matrix 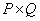can be considered as a system of 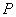equations with 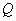unknown. Three cases are possible:

1. The system of equations has a unique solution. 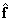, for which .

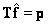2. The system of equations satisfies several solutions.

3. The system of equations does not have an exact solution.

If the system of equations has at least one solution, then it is called joint, and otherwise - incompatible. Systems of equations that do not have solutions are often obtained in the study of physical systems, when the vector 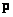describes the sequence of measurements of observable quantities, which by assumption are the result of the impact of some driving force inaccessible for direct observation, represented by the vector 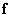. Matrix 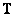is obtained by mathematical modeling of the characteristics of a real system for which the vector 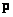is the output signal. When correcting (restoring) images vector 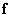usually represents the original image, vector 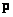- blurred image, and the matrix 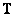describes a discrete mathematical model of the process leading to image blurring. Since the matrix 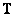and vector 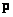usually determined with some error, it may turn out that this vector does not correspond to any of the possible impact vectors .

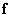We now consider the question of the existence of solutions of the system of equations 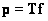. From the structure of the system of equations it is clear that a solution will exist if and only if the vector 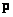can be obtained by a linear combination of matrix columns 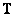. In this case, the vector is said to be 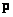lies in the column space of the matrix 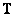. A more rigorous formulation of the condition for the existence of a solution is the following [4]: ​​system of equations 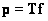has a solution if and only if for the matrix 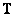there is a conditional inverse matrix 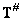satisfying the equation .

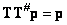So, for the existence of a solution, it is necessary that when mapping from the space of the observed images into the space of the original images (using the conventionally inverse matrix 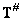) and back (using the matrix 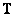) again obtained the vector of observable quantities 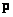. If the system of equations is underdetermined ( 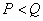), then the solution exists when the rank of the matrix 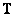equals 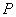i.e. the total number of rows. In all other cases, including the overdetermined system of equations, the existence of a solution must be checked.