Lecture
The probability density or moments of a random field representing an image are often known at the input of some system, and it is required to determine the corresponding characteristics for the image at the output of this system. If the transfer function of the system is represented as an algebraic expression, then the probability density at the output can be found by converting the probability density at the input. For example, let the functions describing the images at the input and output of the system be related as follows:
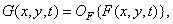 (1.10.1)
(1.10.1)
Where 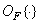 - monotone operator acting on a function
- monotone operator acting on a function 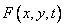 . Then the probability density at the output is
. Then the probability density at the output is
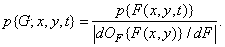 (1.10.2)
(1.10.2)
A transformation of the form (1.10.2) can be extended to high-order probability densities, but often the relations obtained are too cumbersome.
The moments of the random field at the output of the system can be obtained directly if its density probability is known, or in some cases indirectly, based on the properties of the system operator. If, for example, this operator is linear, then the average value of the field 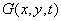 there is
there is
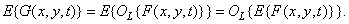 (1.10.3)
(1.10.3)
It can be shown that if the system operator is linear and the random field at the system input is stationary in the strict sense, then the random field at the output is also stationary in the strict sense. If the input field is stationary in a broad sense, then in the same sense the output field is stationary.
Consider a linear space-invariant system, the image at the output of which is represented by the convolution integral:
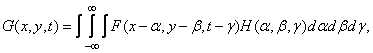 (1.10.4)
(1.10.4)
Where  - impulse response system. Average value
- impulse response system. Average value 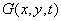 there is
there is
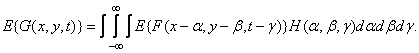 (1.10.5)
(1.10.5)
If the random input field is stationary, then the average 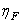 permanently and can be taken out from under the integral. Then
permanently and can be taken out from under the integral. Then
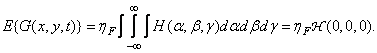 (1.10.6)
(1.10.6)
Where 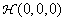 there is a frequency response of a linear system at the origin of the space-time frequency domain. In the same way, it is easy to show that the autocorrelation functions of the input and output fields are related by
there is a frequency response of a linear system at the origin of the space-time frequency domain. In the same way, it is easy to show that the autocorrelation functions of the input and output fields are related by
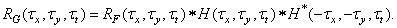 (1.10.7)
(1.10.7)
Performing the Fourier transform of both parts of equality (1.10.7) and using the Fourier convolution theorem, we obtain the relation between the energy spectra of the input and output fields
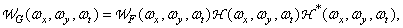 (1.10.8a)
(1.10.8a)
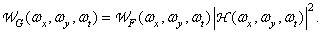 (1.10.8b)
(1.10.8b)
This result will be useful in analyzing the effects of noise in imaging systems.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing