Lecture
In ch. 2 addressed issues related to the mathematical description of continuous images. This chapter provides methods for the formal presentation of discrete images using both deterministic and statistical models.
This section briefly discusses the mathematical operations occurring in the text that are performed with vectors and matrices. The rigorous conclusion and proofs of the theorems and propositions given below can be found in the literature [1–5].
Vector
Column vector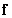 
size 
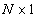is a collection of elements 
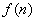where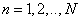 
arranged in a vertical column
(5.1.1)
Line vector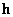 
size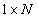 
is an ordered collection of elements 
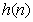where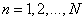 
arranged as a horizontal line
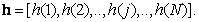(5.1.2)
In the book, bold lowercase letters will usually denote column vectors. The row vector will be denoted as a transposed column vector:
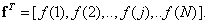(5.1.3)
Matrix
Matrix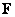 
size 
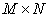is a collection of elements 
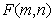Where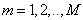 
and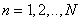 
arranged in the form of rows and columns of a two-dimensional table
(5.1.4)
Symbol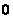 
denotes a zero matrix, all elements of which are equal to zero. The diagonal matrix is a square matrix (when 
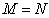), all elements of which are not lying on the main diagonal are zero, i.e. 
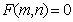, if a 
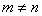. The unit matrix denoted by the symbol 
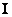, there is a diagonal matrix, all the diagonal elements of which are equal to one. The index at the symbol of the unit matrix indicates its dimensions; 
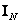denotes a unit size matrix 
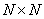. Matrix 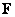can be divided into blocks (submatrices) 
:
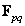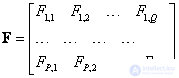. (5.1.5)
Addition of matrices
The sum of two matrices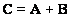 
defined only in the case when both matrices have the same size. Matrix 
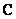- the sum of matrices 
and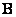 
has dimensions 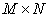and its elements 
.
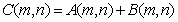Matrix multiplication
The product of two matrices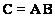 
is defined only when the number of columns of the matrix equal to the number of rows of the matrix 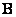. When multiplying the matrix size 
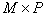to matrix 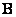size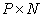 
matrix is obtained 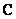size 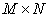whose elements are determined by equality
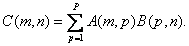(5.1.6)
When multiplying the matrix on the scalar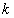 
matrix is obtained 
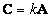whose elements 
.
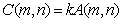Matrix inversion
If a is a square matrix, the inverse matrix and denoted by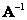 
, has the following properties: 
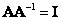and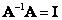 
. If matrix 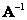exists, then the matrix is called non-singular (non-degenerate). Otherwise, it is called special (degenerate). If some matrix has an inverse, then this inverse matrix is unique. The inverse of the relative inverse matrix coincides with the original matrix, i.e.
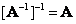(5.1.7)
If matrices and 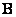non-singular then
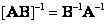(5.1.8)
If the matrix non-singular, but a scalar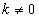 
then
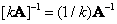. (5.1.9)
The inversion of singular square matrices and non-square matrices will be considered in Ch. 8. Inverse matrix relative to block square matrix
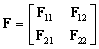, (5.1.10)
can be represented as
(5.1.11)
provided that the matrices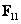 
and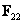 
are not special.
Matrix transposition
When transposing a matrix size 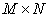size matrix is formed 
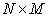which is denoted by 
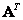. Matrix rows 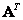match the columns, and the columns match the rows of the matrix . For any matrix
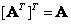. (5.1.12)
If a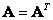 
then the matrix called symmetric. For any matrices and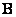
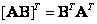(5.1.13)
If the matrix non-singular, then the matrix 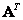also non-singular and
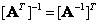. (5.1.14)
Direct matrix product
Left direct product of the matrix size 
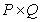to matrix 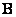size 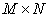is a size matrix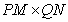 
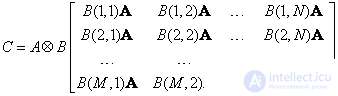. (5.1.15)
Similarly, you can define the right direct product. This book will use only the left direct product. Direct works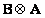 
and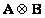 
may vary among themselves. Below are the properties of the operations of multiplication, addition, transposition and inversion of the direct product of matrices:
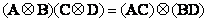, (5.1.16)
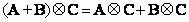, (5.1.17)
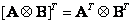, (5.1.18)
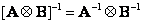, (5.1.18)
Trace matrix
Square matrix trac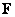e size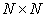 
equal to the sum of its diagonal elements and is denoted as
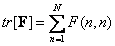. (5.1.20)
If a and 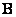- square matrices, then
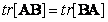. (5.1.21)
The trace of the direct product of two matrices is
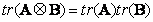. (5.1.22)
Vector norm
Euclidean norm of a vector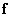 
size 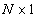called a scalar, defined as
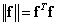. (5.1.23)
Matrix norm
Euclidean norm matrix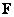 
size 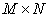called a scalar, defined as follows:
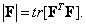. (5.1.24)
Rank matrix
Matrix size 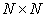has rank 
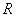if the largest of all its square non-invalid blocks has size 
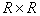. The concept of rank is used when reversing matrices. If matrices and 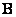non-singular, and 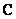is an arbitrary matrix, then
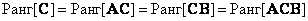. (5.1.25)
Rank matrices and 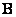satisfies inequalities
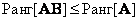, (5.1.26a)
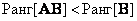. (5.1.26b)
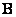Rank of matrix sum and satisfies inequality
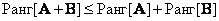. (5.1.27)
Dot product of vectors
Scalar product of vectors 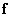and 
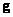size 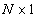is a scalar
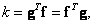(5.1.28)
or
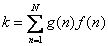. (5.1.29)
Matrix product of vectors
Matrix product of vector 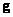size 
by vector 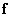size 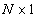is the matrix
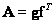(5.1.30)
Where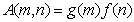 
.
Quadratic form
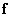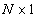Quadratic vector shape size is a scalar
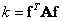, (5.1.31)
Where - size matrix 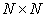. Often the matrix take symmetrical.
Vector derivative
Derivative from scalar product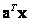 
by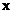 
there is
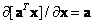, (5.1.32)
and the derivative of the scalar product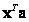 
by vector 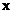equals
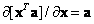. (5.1.33)
Derivative of a quadratic form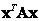 
by 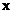there is
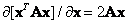. (5.1.34)
Comments
To leave a comment
Digital image processing
Terms: Digital image processing