Lecture
Developing quantitative criteria for faithfulness in reproducing color images is much more difficult than creating such criteria for monochrome images. This is due not only to the increase in the number of quantities describing the image, but also the need to take into account a greater number of psychological factors associated with the perception of colors. The criterion of fidelity for reproducing color images should be consistent with the measure of color difference and such phenomena as Mach color stripes and color adaptation.
In section 7.3.2 an expression for the measure of color difference was obtained.
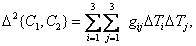 (7.5.1)
(7.5.1)
Where 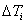 , denotes the difference of color coordinates, a
, denotes the difference of color coordinates, a 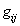 - weights depending on the coordinates of the color. Based on this formula, we take the normalized root-mean-square error as the criterion for the faithfulness of reproducing color images. By definition, this measure is
- weights depending on the coordinates of the color. Based on this formula, we take the normalized root-mean-square error as the criterion for the faithfulness of reproducing color images. By definition, this measure is
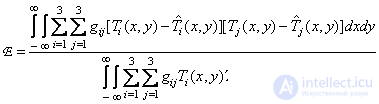 , (7.5.2)
, (7.5.2)
Where 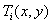 and
and  - color components of the reference and distorted images, respectively. The root-mean-square error is quite difficult to calculate using this formula, since it includes cross-member products of different color coordinates. In addition, weights
- color components of the reference and distorted images, respectively. The root-mean-square error is quite difficult to calculate using this formula, since it includes cross-member products of different color coordinates. In addition, weights 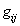 not constant, but depend on the coordinates of the color. As noted when considering the color metric, there is no such linear transformation in which the cross terms disappear completely. With the help of nonlinear coordinate transformations described in Ch. 3, transition to color space
not constant, but depend on the coordinates of the color. As noted when considering the color metric, there is no such linear transformation in which the cross terms disappear completely. With the help of nonlinear coordinate transformations described in Ch. 3, transition to color space 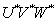 or
or 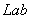 temporarily adopted by the ICE as standard spaces with a uniform distribution of brightness and chromaticity. In space
temporarily adopted by the ICE as standard spaces with a uniform distribution of brightness and chromaticity. In space 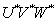 For example, the expression for the root-mean-square error is
For example, the expression for the root-mean-square error is
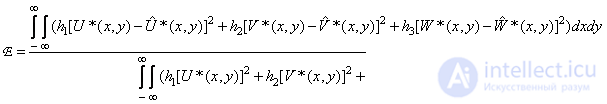 (7.5.3)
(7.5.3)
With a different approach to the choice of the mean square measure of fidelity for reproducing a color image, color coordinates that are uncorrelated with each other are used as a result of the transformation of the primary coordinates. Such a decorrelation can be carried out using the Karhunen – Loev decomposition described in Ch. 3. The disappearance of cross-members in the measure thus obtained is intuitively justified by the fact that the color coordinates are statistically uncorrelated. The Karhunen – Loeve transformation is defined by the covariance matrix of color coordinates 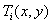 source image, which must either be measured (estimated) or obtained from the model of this class of color images. Coordinate system
source image, which must either be measured (estimated) or obtained from the model of this class of color images. Coordinate system 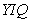 turned out to be rather close to the Karunen – Loeve system [38]. For this reason, the rms error calculated for the coordinates
turned out to be rather close to the Karunen – Loeve system [38]. For this reason, the rms error calculated for the coordinates 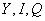 It is often used as a measure of fidelity for reproducing color images. Unfortunately, there is not enough data to judge the consistency of the measures discussed in this section with the results of subjective assessments.
It is often used as a measure of fidelity for reproducing color images. Unfortunately, there is not enough data to judge the consistency of the measures discussed in this section with the results of subjective assessments.
The third way to determine the fidelity of reproducing color images is to calculate the root-mean-square error in the geodesic color space, consistent with some human color vision model. For a similar model shown in Fig. 2.5.3, the standard error is
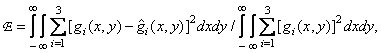 (7.5.4)
(7.5.4)
Where 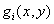 - signals received from cone signals
- signals received from cone signals 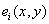 using the following transformations:
using the following transformations:
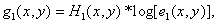 (7.5.5a)
(7.5.5a)
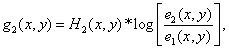 (7.5.5b)
(7.5.5b)
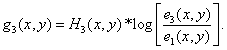 (7.5.5b)
(7.5.5b)
Variables 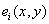 in turn related to color coordinates
in turn related to color coordinates 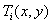 some linear transformation
some linear transformation
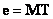 , (7.5.6)
, (7.5.6)
Where 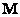 - size conversion matrix
- size conversion matrix 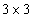 . As in the previous cases, there was almost no experimental verification of the suitability of the geodesic measure of error.
. As in the previous cases, there was almost no experimental verification of the suitability of the geodesic measure of error.
The above measures of fidelity for reproducing continuous color images can also be adapted for evaluating discrete color images using the technique used to sample the fidelity measures for reproducing monochrome images.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing