Lecture
In section 1.4, the concepts of linearity and superposition were introduced in order to extend the concept of linearity to a wider class of systems.
Consider two functions describing images, 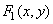 and
and 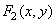 which, interacting in some way
which, interacting in some way  give function
give function 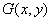 :
:
 . (1.8.1)
. (1.8.1)
Let be 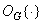 - operator of the system that transforms
- operator of the system that transforms 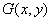 , which has the following properties:
, which has the following properties:
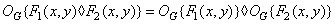 (1.8.2a)
(1.8.2a)
and
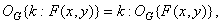 (1.8.2b)
(1.8.2b)
Where 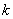 is a constant, and the colon denotes a generalized multiplication by a constant. In [4] it is shown that if the operation
is a constant, and the colon denotes a generalized multiplication by a constant. In [4] it is shown that if the operation 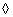 is reduced to adding vectors, and the operation: - to multiplying a vector by a scalar, then the operator
is reduced to adding vectors, and the operation: - to multiplying a vector by a scalar, then the operator 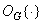 can be represented as a chain of operators, called a homomorphic filter (Fig. 1.8.1). First operator
can be represented as a chain of operators, called a homomorphic filter (Fig. 1.8.1). First operator 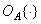 turns operations
turns operations 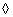 and: in addition of vectors and multiplication of a vector by a scalar:
and: in addition of vectors and multiplication of a vector by a scalar:
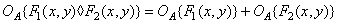 (1.8.3a)
(1.8.3a)
and
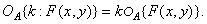 (1.8.3b)
(1.8.3b)
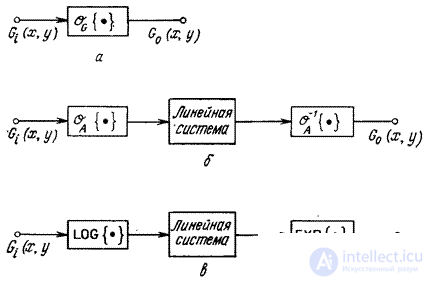
Fig. 1.8.1. Generalized linear systems: a - generalized system; b - representation of the generalized system as a homomorphic filter; в - multiplicative homomorphic filter.
The second stage of a homomorphic filter is a regular linear system. Third Stage - Operator 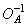 which is the reverse of the first operator, i.e.
which is the reverse of the first operator, i.e.
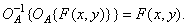 (1.8.4)
(1.8.4)
Fig. 1.8.1, in illustrates a particular case of a homomorphic filter for a multiplicative system [5], in which the function 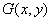 is obtained by multiplying the functions
is obtained by multiplying the functions 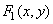 and
and 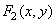 i.e.
i.e.
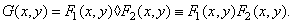 (1.8.5)
(1.8.5)
Prologized by both sides of equality (1.8.5), we obtain the sum of the logarithms of the functions 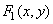 and
and 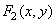 :
:
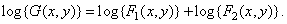 (1.8.6)
(1.8.6)
Function 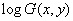 is transformed by some linear system, and then returns to the source image space by means of an exponential transformation. The operation of generalized multiplication of a vector by a scalar is defined as exponentiation
is transformed by some linear system, and then returns to the source image space by means of an exponential transformation. The operation of generalized multiplication of a vector by a scalar is defined as exponentiation
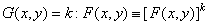 (1.8.7)
(1.8.7)
Logging this equation gives
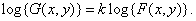 (1.8.8)
(1.8.8)
The use of homomorphic filtering for image restoration is discussed in Ch. 15.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing