Lecture
From expressions (3.4.7) it follows that the set of primary colors can be chosen in many ways. If color coordinates are known for one set of primary colors, then a simple coordinate transformation can be used to find color coordinates for another set [16]. Let be 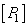 ,
, 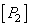 ,
, 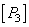 there is an initial set of primary colors with spectral densities
there is an initial set of primary colors with spectral densities 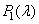 ,
, 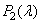 ,
, 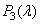 . Intensities Equalizing Reference White
. Intensities Equalizing Reference White 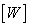 denote by
denote by 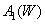 ,
, 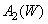 and
and 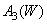 . Consider now another set of primary colors.
. Consider now another set of primary colors. 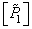 ,
, 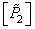 ,
, 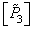 having spectral densities
having spectral densities  ,
, 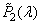 ,
, 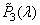 . Reference white color
. Reference white color  which may differ from the original reference white
which may differ from the original reference white 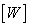 equalized with intensities
equalized with intensities 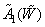 ,
, 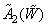 ,
, 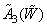 new colors. Arbitrary color
new colors. Arbitrary color 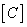 has coordinates
has coordinates 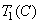 ,
, 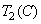 ,
, 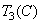 for the initial set of primary colors and
for the initial set of primary colors and 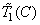 ,
, 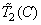 ,
, 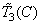 for a new set. From the formula (3.4.10) you can get the matrix ratio
for a new set. From the formula (3.4.10) you can get the matrix ratio
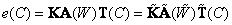 . (3.5.1)
. (3.5.1)
Let us now establish the units of measurement for the new color coordinates. Taking instead of color 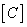 new reference white color
new reference white color  will get
will get
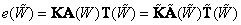 , (3.5.2)
, (3.5.2)
Where 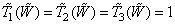 . Then substituting the new primary colors into the ratio (3.5.1)
. Then substituting the new primary colors into the ratio (3.5.1) 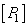 ,
, 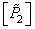 ,
, 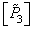 , will have
, will have
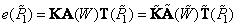 , (3.5.3a)
, (3.5.3a)
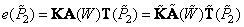 , (3.5.3b)
, (3.5.3b)
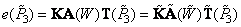 , (3.5.3b)
, (3.5.3b)
Where
 ,
,  ,
,  .
.
The joint solution of the system of matrix equations (3.5.1), (3.5.2) and (3.5.3) gives the required relationship between the color coordinates for the original and the new sets of primary colors:
 (3.5.4)
(3.5.4)
You can rewrite the relation (3.5.4) using the chromaticity coordinates 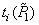 ,
, 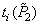 ,
, 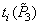 New primary colors in the coordinate system of the original primary colors. In this case
New primary colors in the coordinate system of the original primary colors. In this case
 , (3.5.5)
, (3.5.5)
Where
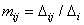 ,
,
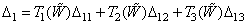 ,
,
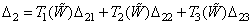 ,
,
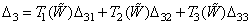 ,
,
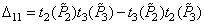 ,
,
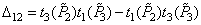 ,
,
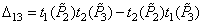 ,
,
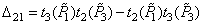 ,
,
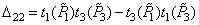 ,
,
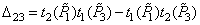 ,
,
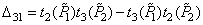 ,
,
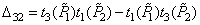 ,
,
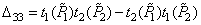 .
.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing