1.9. PROBABLE DESCRIPTION OF CONTINUOUS IMAGES

It is often convenient to consider the image as the implementation of a random process. We introduce a continuous random function generating images 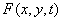three variables - spatial coordinates 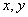and time .

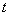Random process 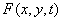fully described by joint probability density

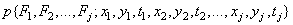
for 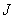function values 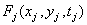in points of reference 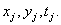High order joint probability densities for images are usually not known, and they are generally difficult to model. For probability density first order 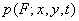sometimes it is possible to select a successful model from physical considerations or on the basis of measured histograms. For example, the probability density of the first order of random noise in electronic image converters is well modeled by a Gaussian density:

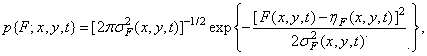(1.9.1)

where are the parameters 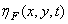and 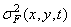there is a mean and variance of noise. Gaussian density can also, with acceptable accuracy, serve as a probability density model for unitary image transformation coefficients. The probability density of the brightness should be one-sided, since the brightness takes only positive values. Rayleigh probability density distributions are used as brightness probability density models.

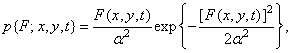(1.9.2a)

log-normal density

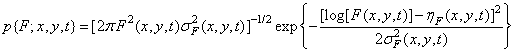(1.9.2b)

and exponential density

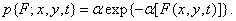(1.9.2в)

These densities are determined at 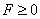, and 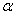- constant. Bilateral exponential, or Laplace, density

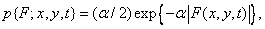(1.9.3)

Where 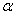- constant, often used as a model of probability density difference of samples of the function describing the image. Finally, uniform density

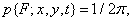
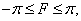(1.9.4)

There is a conventional model for fluctuations in the phase of a random process. To describe a random process, conditional probability densities can also be used. Conditional probability density of the function value 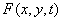at the point 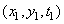for a given value of this function at 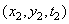defined as

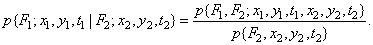(1.9.5)

The conditional densities of a higher order are determined similarly.

Another way to describe a random process is to calculate averages over an ensemble. The first moment, or the mean value of the function 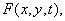equals

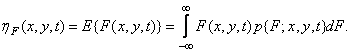(1.9.6)

The second moment, or autocorrelation function, is defined as

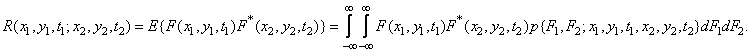(1.9.7)

The image autocovariance function is defined as

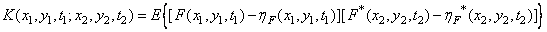(1.9.8a)

Autocovariance and autocorrelation functions are related by

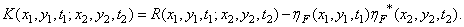(1.9.8b)

finally the process variance 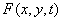there is

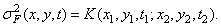(1.9.9)

A random process that generates images is called stationary in the strict sense if its moments do not depend on the transfer of the origin of coordinates in space or time. The process is called stationary in a broad sense, if it has a constant average brightness, and its autocorrelation function depends on the difference of coordinates 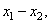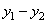, 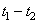but not from the coordinates themselves. For stationary process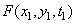

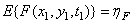(1.9.10a)

and

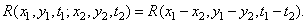(1.9.10b)

The expression for the autocorrelation function can be written as

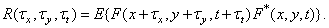(1.9.11)

Because

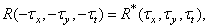(1.9.12)

for real function 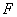the autocorrelation function is real and even. The energy spectrum of a stationary image, by definition, is the result of a three-dimensional Fourier transform of its autocorrelation function:

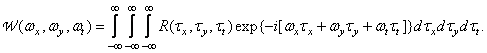(1.9.13)

In many imaging systems, spatial and temporal imaging processes are separated. In this case, the stationary autocorrelation function can be written as

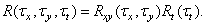(1.9.14)

Often, to simplify the calculations, the spatial autocorrelation function is presented as a product of autocorrelation functions for each spatial variable:

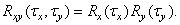(1.9.15)

In the images of objects created by man, horizontal and vertical structures are often found, therefore, the approximation of the autocorrelation function by the product (1.9.15) is quite acceptable. In images of natural scenes there are usually no prevailing correlation directions. The spatial autocorrelation function of such images is close to the function with rotational symmetry and is therefore not separable.

Often the model of the image are the implementation of a two-dimensional Markov process of the first order. The autocovariation function of such a process is

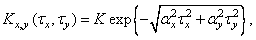(1.9.16)

Where 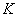, 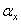and 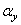- scale factors. The corresponding energy spectrum is

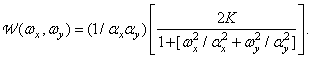(1.9.17)

Often, a simplifying assumption is made that the autocovariance function of a Markov process can be represented as

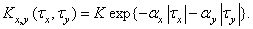(1.9.18)

The energy spectrum of this process is

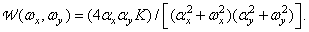(1.9.19)

When a deterministic description of the images were determined by the average in space and time. The statistical description also determines the ensemble average. The question arises: how are the space-time averages and ensemble averages related to each other? The answer is that for some random processes, called ergodic, the space-time averages and averages over the ensemble are equal. It is very difficult to prove the ergodicity of a random process in the general case. It is usually sufficient to determine the second-order ergodicity, at which the first and second-order moments obtained by space-time averaging are equal to the corresponding moments when averaged over the ensemble.