8.5. SOLUTION OF JOINT SYSTEMS OF LINEAR EQUATIONS

Having established the existence of a solution to the system of equations

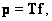(8.5.1)

it is necessary to determine the nature of the decision: is it unique or is there several solutions, and what kind of solution does it have? The answer to the last question is contained in the following fundamental theorem [4]:

If solving a system of equations 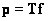exists, then in general it looks like

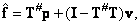(8.5.2)

Where 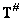- matrix, conventionally inverse with respect to the matrix 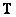a 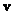- arbitrary size vector .

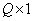For proof, multiply both sides of (8.5.2) by the matrix :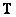

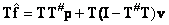(8.5.3)

However, by the condition of the existence of a solution 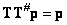. Furthermore, according to the definition of the conditionally inverse matrix, 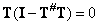. Consequently, 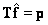and vector 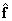is a solution.

Insofar as 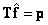, then, multiplying both sides of this equality by the matrix 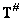get

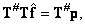(8.5.4a)

or

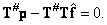(8.5.4b)

Adding a vector to both parts 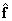get

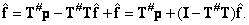(8.5.5)

This result coincides with the relation (8.5.2) if the vector 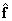standing on the right side of formula (8.5.5), replace with an arbitrary vector .

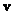Since the generalized inverse matrix 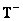and matrix 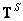since the least squares inversions are conditionally inverse, then the general solution of system (8.5.1) can also be represented as

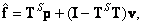(8.5.6a)

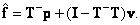(8.5.6b)

The solution will obviously be the only one 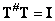. Bo all such cases 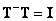. Examining the rank of the matrix 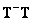, it is possible to prove that [4] if the solution of the system of equations 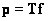exists that it is unique if and only if the rank of the matrix 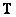size 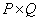equals .

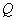It follows that if a solution to the underdetermined system of equations exists, then it is not unique. On the other hand, an overdetermined system of equations can have only one solution.

Let the exact solution for the system of equations (8.5.1) be obtained. Consider the assessment

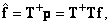(8.5.7)

Where 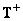denotes one of the pseudoinverse matrices with respect to 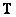which will not necessarily coincide with this solution, since the product of the matrices 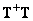may not equal the unit matrix. The magnitude of the error, i.e. the deviation of the estimate 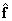from true value 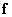, usually expressed in terms of the square of the difference of the vectors 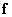and 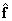in the form of a work

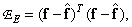(8.5.8a)

or how

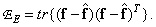(8.5.8b)

Substituting expression (8.5.7) into (8.5.8a), we obtain

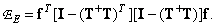(8.5.9)

Matrix value 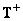at which the error (8.5.8) turns out to be minimal, can be found by equating to zero the derivative of the error 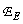by vector 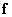. According to the relation (5.1.34),

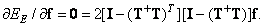(8.5.10)

Equality (8.5.10) is satisfied if the matrix 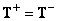i.e. is a generalized inverse matrix with respect to 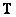. In this case, the estimation error is reduced to a minimum equal to

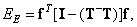(8.5.11a)

or

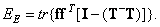(8.5.11b)

As expected, the error becomes zero when 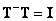. This will happen, for example, if the generalized inverse matrix 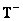has rank 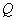and is determined by the ratio (8.3.5