Lecture
Transformation processing can be successfully applied to obtain generalized inverse matrices. As can be seen from the relation (11.1.6b), the matrix 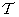 linear operator in spectral space is associated with an arbitrary matrix
linear operator in spectral space is associated with an arbitrary matrix 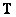 size
size 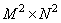 in the following way:
in the following way:
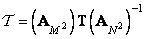 . (11.5.1)
. (11.5.1)
In the same notation, the generalized inverse matrix 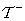 defined as
defined as
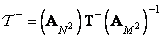 , (11.5.2)
, (11.5.2)
Where 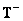 - size matrix
- size matrix 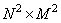 . Relations (11.5.1) and (11.5.2) are self-consistent, since it is known that for an arbitrary matrix
. Relations (11.5.1) and (11.5.2) are self-consistent, since it is known that for an arbitrary matrix 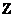 and unitary matrices
and unitary matrices 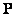 and
and 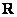 equality is fulfilled
equality is fulfilled 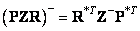 [13, p. 100].
[13, p. 100].
If the rank of the matrix 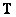 equals
equals 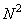 , then, according to the formula (8.3.5),
, then, according to the formula (8.3.5),
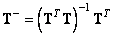 (11.5.3)
(11.5.3)
and it is not difficult to show that
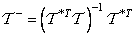 . (11.5.4)
. (11.5.4)
In the opposite case, when the rank of the matrix 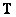 equals
equals 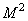 , from the formula (8.3.6) it follows that
, from the formula (8.3.6) it follows that
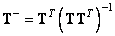 (11.5.5)
(11.5.5)
and the generalized inverse transformation matrix in the spectral space satisfies the relation
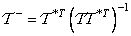 . (11.5.6)
. (11.5.6)
We indicate, for example, that the generalized inverse matrices with respect to matrices of maximal rank corresponding to the superposition operators 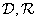 and
and 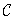 determined by equalities
determined by equalities
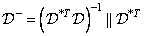 , (11.5.7а)
, (11.5.7а)
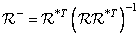 , (11.5.7b)
, (11.5.7b)
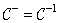 . (11.5.7b)
. (11.5.7b)
In fig. 11.5.1 shows printouts of generalized inverse matrices for convolution operators of one-dimensional signals using Fourier and Hadamard transforms. It is well seen that these matrices are more sparse than the original matrices. Moreover, the generalized inverse matrix of the cyclic convolution operator with the Fourier transform is diagonal, since, as follows from (11.2.13), the matrix 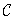 - diagonal.
- diagonal.

Fig. 11.5.1. Generalized inverse matrices of convolution operators of one-dimensional signals using Fourier and Hadamard transforms.
a is the final convolution; b - discretized integral convolution; c is a cyclic convolution.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing