11.6. RECURSIVE FILTRATION

In the previous sections of this chapter, transformation processing was considered as an indirect method for performing two-dimensional linear processing. It has been shown that conversion processing often requires much less arithmetic than with standard methods. In this section, another linear processing method called recursive filtering will be considered [14–16]. Sometimes recursive filtering is even more efficient than processing with conversion. In addition, in this case, data storage requires a smaller storage capacity than during processing with conversion.

Recursive filtering is based on a recurrent relationship between system input and output variables. For one-dimensional signals, the following recurrence relation has the following form [14]:

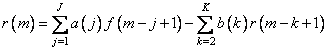, (11.6.1)

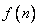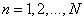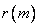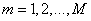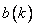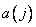Where , - samples of the input sequence, , - samples of the output sequence, and and - weight factors. The key point here is that 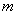th element of the output sequence depends not only on the last and 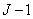the penultimate elements of the input sequence, but also from 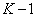previous elements of the output sequence.

Most methods of synthesis and analysis of recursive filters are based on the use of 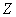-conversion. By definition [17, 18] 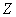-transformation 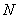-element sequence 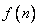gives an image

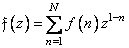. (11.6.2)

It is not difficult to show that 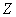-transformation of expression (11.6.1) gives the image

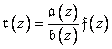, (11.6.3)

Where 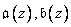and 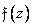- images of the corresponding sequences.

Two-dimensional recursive filtering is based on the following recurrent relationship between the input and output arrays [19, 20]:

(11.6.4)

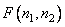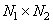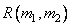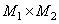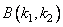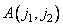Where - input array from elements - output array from elements as well and - weight factors. It is assumed that the recursive filtering process starts from the upper left corner of the input array. Using two-dimensional 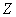-transformations from equality (11.6.4) is obtained

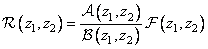, (11.6.5)

Where 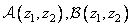and 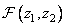- two-dimensional images of the corresponding arrays. For example,

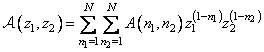. (11.6.6)

During the synthesis of recursive filters, it is required to choose such arrays of weighting factors. 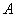and 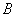to output array 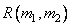turned out to be equivalent to the array resulting from the convolution of the function 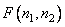describing the original image with a given impulse response 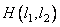. As a rule, an exact coincidence of arrays cannot be achieved, and it is necessary to use approximate methods in the synthesis of filters [21, 22]. This raises the question of the stability of the calculated recursive filter. If the filter is unstable, then rounding errors or noise present in the input array may not be attenuated during processing, but may increase to a very large level. A recursive filter is stable [20] if the coefficients 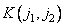expansion of the frequency response of the filter in a series in powers of the variables 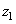and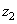

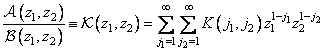(11.6.7)

are absolutely summable, i.e., they satisfy the condition

. (11.6.8)

Several methods of testing recursive filters for stability have been developed [23–25]. When processing the image according to equality (11.6.4) is required

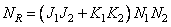(11.6.9)

arithmetic operations. Here 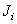and 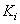- sizes of arrays of weight factors for the input and output images, a 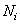- dimensions of the input image. If the images and arrays of the weighting factors are square (i.e. 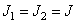, 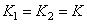and 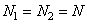), then with recursive filtering you need to run

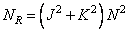(11.6.10)

operations. For comparison, we point out that to obtain the final convolution (see Section 9.3) it is required

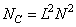(11.6.11)

operations where 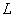- the size of the impulse response. As shown in sect. 11.2, to obtain convolution using the fast Fourier transform, approximately

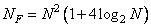(11.6.12)

operations. The degree of relative efficiency of the three types of processing depends on the size of the pulse response array [27]. If these dimensions are small, then a direct number of arithmetic operations is required for the direct method of obtaining convolution and recursive filtering. In this case, it is possible to compare the effectiveness of both methods with the efficiency of obtaining convolution using FFT using the graph in fig. 11.3.2. For large sizes of the impulse response array, the fast method of obtaining convolution turned out to be much more efficient than the direct method. Comparing the number of operations in equalities (11.6.10) and (11.6.12), it can be shown that with large impulse response sizes, recursive filtering turns out to be more efficient than the fast method of obtaining convolution if the areas of the arrays of the recursive filter satisfy the inequality

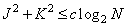, (11.6.13)

Where 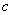- constant, taking values ​​from 1 to 20, and its value depends on the type of FFT algorithm used and on how much the calculations with complex numbers occur more slowly than with real ones.