9.4. RELATIONSHIP BETWEEN LINEAR OPERATORS

From the matrix of the cyclic superposition operator 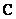It is possible to obtain the matrices of the superposition operator 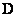and discretized superposition operator 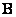. To do this, enter the selection matrix

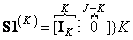, (9.4.1а)

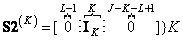, (9.4.1b)

Where 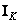- unit size matrix 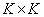. We give the relations connecting these matrices with matrices obtained from them by generalized inversion and transposition:

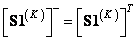, (9.4.2а)

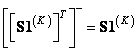, (9.4.2b)

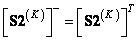, (9.4.2в)

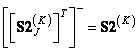. (9.4.2g)

Analyzing the structure of various linear operators, we can show that

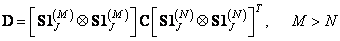, (9.4.3а)

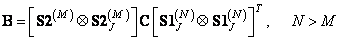. (9.4.3b)

So the matrix 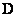formed by highlighting the first 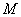rows and 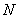block columns 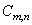matrices 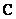. At the same time, in all other blocks, the first 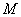rows and 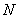columns. Similarly from the matrix 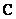can form a matrix 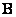. Matrix elements 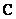which matrices are forme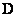d and 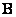in fig. 9.3.1, and enclosed in frames.

From the definition (9.3.1) of the extended array of samples of the original image, it follows that the vector of samples of the final source image 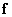formed from the vector of the extended image 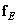using the allocation operation:

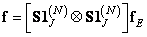, (9.4.4а)

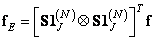. (9.4.4b)

It can also be shown that the output vector of the superposition operator of finite arrays can be obtained from the output vector of the cyclic superposition operator using the extraction operation:

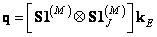. (9.4.5a)

There is an inverse relationship between vectors.

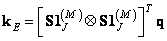. (9.4.5b)

For a discretized superposition operator

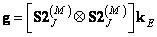, (9.4.6)

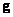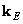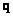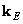however the reverse transition from to cannot be performed due to the underdetermined discretized superposition operator. Transforming and in the matrix form, from the relation (9.4.5а) it is possible to obtain the equality

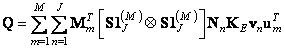. (9.4.7)

Since the selection operator has the property of separability, the formula (9.4.7) is simplified to the form

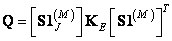. (9.4.8)

Similarly, from equality (9.4.6) relating to the discretized superposition operator, one can obtain the relation

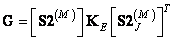. (9.4.9)

In fig. 9.4.1 shows the location of the elements of the matrix 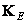the matrices for the superposition operator of finite arrays are formed 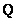and for the discretized superposition operator .

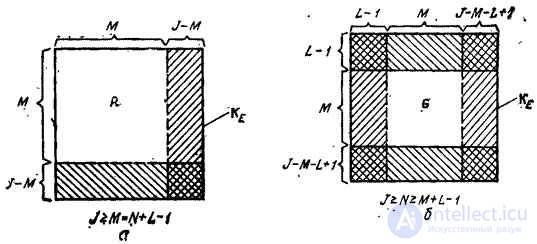
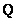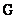Fig. 9.4.1. Location of the matrices and in the matrix .

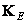a is a superposition operator of finite arrays; b - discretized superposition operator.

So, for both operators, output vectors can be obtained from the result of cyclic superposition using the operation of extracting a part of the elements. As shown in Ch. 11, this fact allows us to simplify the calculations.