1.4. LINEAR OPERATORS

A two-dimensional system is called linear if the superposition principle holds for it. In the particular case of mapping a function into a function, this requires that

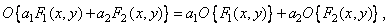(1.4.1)

Where 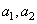- some constants (can be complex). The definition of the property of superposition can be easily extended to the general form (1.2.1).

Using the property of the delta function (1.3.1g), the function at the input of the system 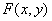can be represented as a weighted sum of delta functions:

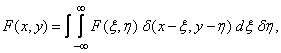(1.4.2)

Where 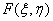- weight factor delta pulse having coordinates 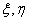on surface 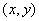(Fig. 1.4.1). If the function at the output of the linear system

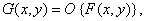(1.4.3)

that

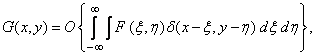(1.4.4a)

or

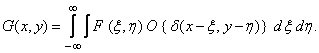(1.4.4b)

To go from the expression (1.4.4a) to (1.4.4b), the order of the operations of linear transformation and integration was changed. The linear operator acted only on that multiplier of the integrand (1.1.4a), which depends on the spatial variables 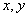. We write the second multiplier of the integrand (1.4.4b) as

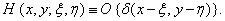(1.4.5)

We will call this function the impulse response of a two-dimensional system. The impulse response of the optical system is often called the point spread function.

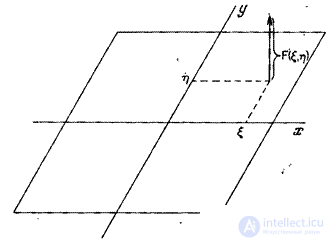
Fig. 1.4.1. Representation of a function describing an image as a superposition of delta functions.

Substituting the impulse response in relation (1.4.4b) gives the integral of the superposition

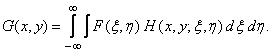(1.4.6)

A linear two-dimensional system is called spatially invariant (isoplanatic) if its impulse response depends only on the difference of coordinates 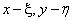. For the optical system shown in fig. 1.4.2. This means that when moving a point source in the object plane, the image of this source in the focus plane will also change its position, but retain its shape. For spatially invariant system

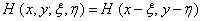(1.4.7)

and the superposition integral has a special form, called the convolution integral:

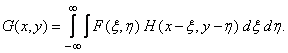(1.4.8a)

Convolution operations are symbolically written as

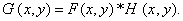(1.4.8b)

The convolution integral is symmetric, i.e.

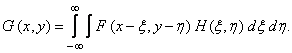(1.4.9)

The convolution process is illustrated in Fig. 1.4.3. In fig. 1.4.3, a and 1.4.3, b depicts the function 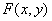input and impulse response.

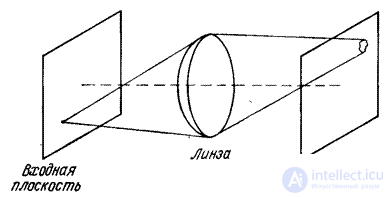
Fig. 1.4.2. Image of a point source of light in the optical system.

In fig.1.4.3, the impulse is shown: the response when the coordinates are reversed, and in fig. 1.4.3, g - with a shift by 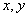. In fig. 1.4.3, d shaded the area in which the product 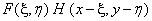included in the integrand (1.4.8, a) is not equal to zero. Integration on this area gives the value 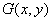for given coordinate values 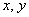. So the function 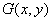at the output, it can be found by scanning the input function by a sliding “window” - reversed impulse response, and integration over the area in which these functions overlap.

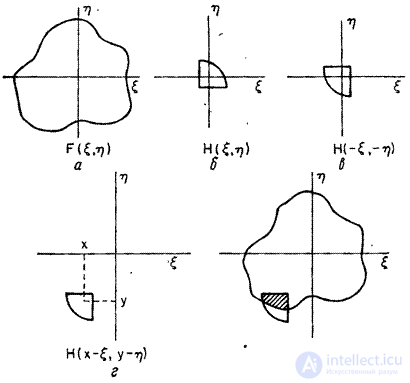
Fig. 1.4.3. An example of two-dimensional convolution.