Content
Introduction
Linear convolution
Cyclic convolution
Algorithm for fast calculation of convolution based on FFT
findings
Introduction
One of the radio engineering whales is undoubtedly the convolution operation:
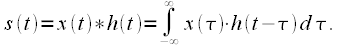 |
(one) |
Convolution allows you to calculate the signal
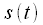
at the output of the linear filter with impulse response
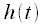
, at the input signal
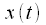
.
In the discrete case, there are two types of convolutions: linear (or aperiodic) and cyclic. Cyclic convolution is often referred to as circular or periodic.
Linear convolution
Consider a linear convolution. Let there be two discrete signals.
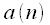
,
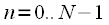
and
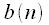
,
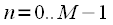
. In general, the length of these signals
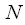
and
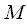
may differ. Linear convolution of signals
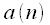
and
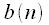
called a discrete signal of the form:
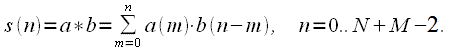 |
(2) |
To calculate linear convolution signals
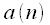
and
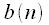
shift relative to each other termwise multiply and fold. It is assumed that
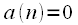
at
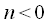
and

, and
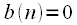
at
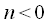
and
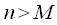
A graphical representation of linear convolution is presented in Figure 1.
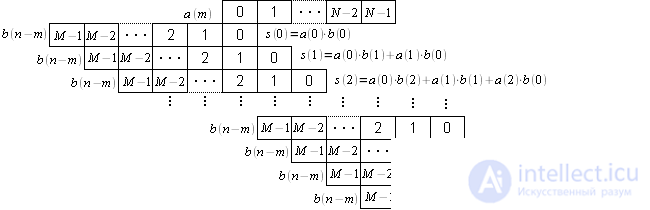
Figure 1: Graphical representation of linear convolution
Signal counts
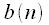
shift relative to the sequence counts
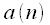
all possible overlapping counts multiply together and add up.
Figure 2 shows an example of calculating the linear convolution of two signals.
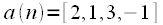
4 counts long
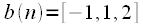
3 counts long.
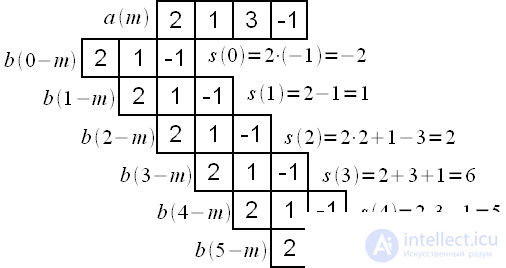
Figure 2: Example of a linear convolution calculation.
It should be noted that the signal
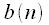
when calculating the convolution is reflected from left to right, because
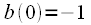
the very first count (the earliest in time) and it should also be processed first.
Cyclic convolution
We now consider cyclic convolution. In the case of cyclic convolution, it is assumed that discrete signals
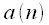
and
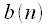
- periodic with the same period
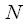
counts. Then circular convolution of the signals
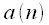
and
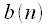
called the signal type:
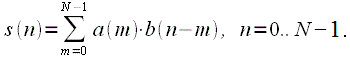 |
(3) |
The result of cyclic convolution also has a length
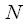
counts.
Consider a cyclic convolution using the example of two signals.
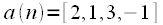
and
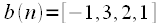
. Graphically, the calculation of cyclic convolution is presented in Figure 3.
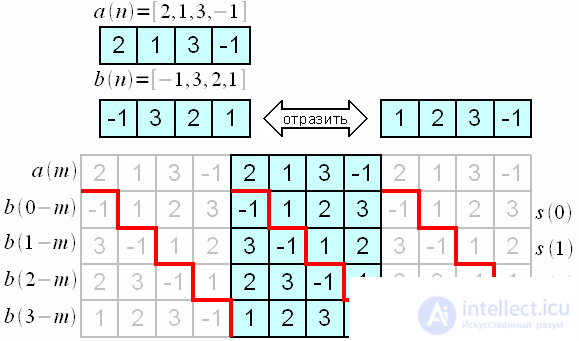
Figure 3: Calculating the circular convolution
The red line marks the boundaries of the repetition periods.

. Note that due to the periodicity of the signals
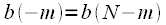
.
Calculate the convolution step by step:
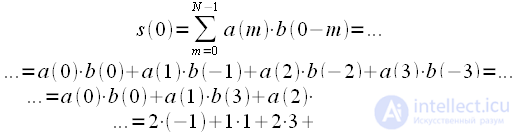 |
(four) |
Now let's calculate
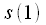
:
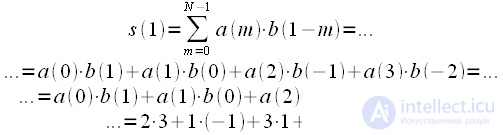 |
(five) |
Similarly, you can calculate
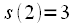
and
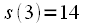
.
Using cyclic convolution, one can calculate the linear convolution of two signals. This requires each of the signals
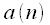
and
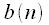
duration
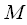
and
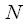
counts respectively add zeros to length
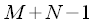
.
We give an example of calculating a linear convolution through a cyclic for
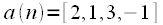
4 counts long
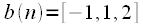
3 references long (this example was considered above).
We add zeros
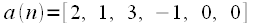
and
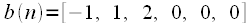
, so that in each sequence was 6 samples.
Calculate the cyclic convolution as shown in Figure 4.
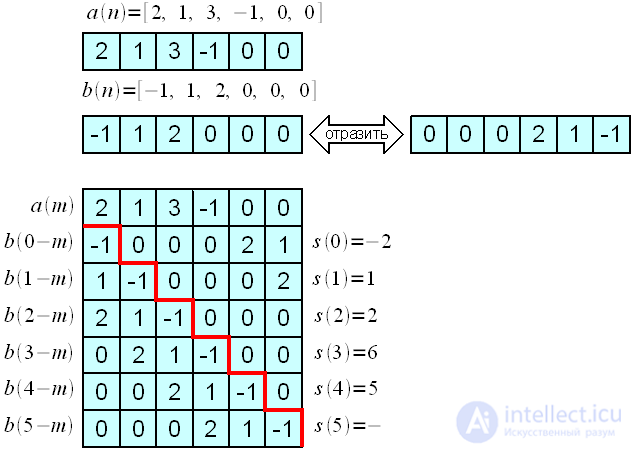
Figure 4: Calculating linear convolution through cyclic <
You can compare with the result of the very first example for linear convolution and make sure that the values match.
Algorithm for fast calculation of convolution based on FFT
At first glance it may seem that the calculation of linear convolution through cyclic does not make sense, since it does not reduce the calculation. Valid to calculate linear convolution required
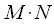
multiplications
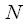
and
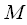
- the length of the convolved signals, and when calculating a linear convolution through a cyclic
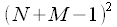
multiplications and additions. However, consider the discrete Fourier transform of cyclic convolution:
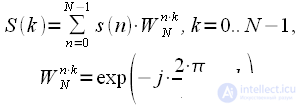 |
(6) |
Substituting the expression for cyclic convolution we get:
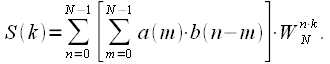 |
(7) |
Swap the summation operations:
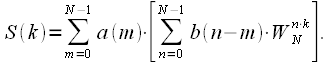 |
(eight) |
Imagine a multiplier
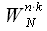
as:
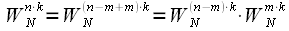 |
(9) |
Substituting (9) into (8) we get:
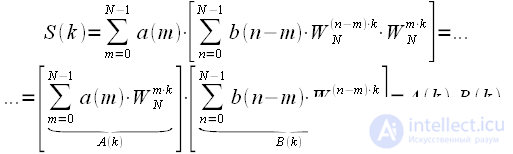 |
(ten) |
Thus, the cyclic convolution spectrum is the product of the spectra of the convolved signals, and the Fast Fourier Transform (FFT) algorithm can be used to calculate it. Thus, the circuit for calculating cyclic convolution can be represented in Figure 5:
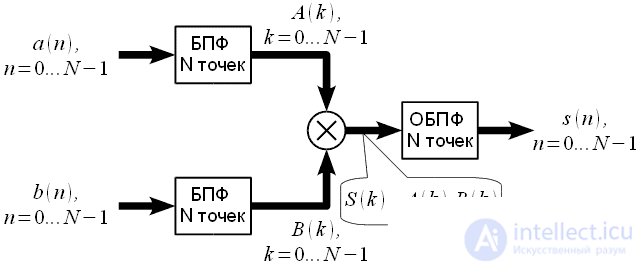
Figure 5: Calculating cyclic convolution using FFT
Since effective FFT algorithms do not exist for all lengths
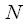
then we can propose the following method for calculating cyclic convolution. Source sequences
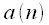
and
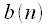
,
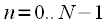
can be filled with zeros to length
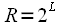
Since for effective lengths of an integer power of two, efficient FFT algorithms have been developed, then we apply the convolution calculation scheme presented in Figure 5. At the output, we obtain
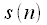
,
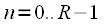
from which you need to take only the first
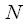
counts.
Similarly, you can do when calculating linear convolution through cyclic.
Consider an example. Let be
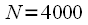
, but
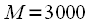
. Direct linear convolution calculation will require
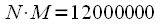
(12 million) multiplication and addition operations.
Fill in each of the sequences up to 8192 samples with zeros and apply the FFT algorithm with decimation by time, then the calculation of one FFT will be required
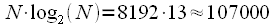
complex multiplication operations or 428000 real multiplication operations. There will be only 3 such blocks of FFT, plus you need to take into account 8192 complex multiplications of the spectra, total
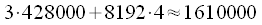
, which is almost 7.5 times lower than if we considered linear convolution in the forehead.
findings
Thus, we considered two types of discrete convolutions: linear and cyclic; we established a connection between them. It has been shown that the use of FFT provides a significant reduction in computational operations when calculating both cyclic and linear convolutions.
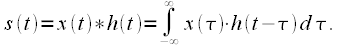
 at the output of the linear filter with impulse response
at the output of the linear filter with impulse response 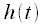 , at the input signal
, at the input signal 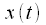 .
.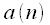 ,
, 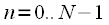 and
and 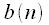 ,
, 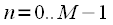 . In general, the length of these signals
. In general, the length of these signals 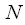 and
and 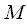 may differ. Linear convolution of signals
may differ. Linear convolution of signals 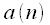 and
and 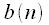 called a discrete signal of the form:
called a discrete signal of the form: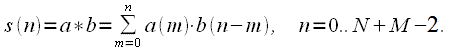
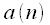 and
and 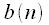 shift relative to each other termwise multiply and fold. It is assumed that
shift relative to each other termwise multiply and fold. It is assumed that 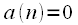 at
at 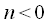 and
and  , and
, and 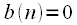 at
at 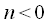 and
and 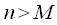

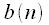 shift relative to the sequence counts
shift relative to the sequence counts 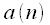 all possible overlapping counts multiply together and add up.
all possible overlapping counts multiply together and add up.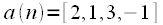 4 counts long
4 counts long 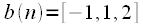 3 counts long.
3 counts long.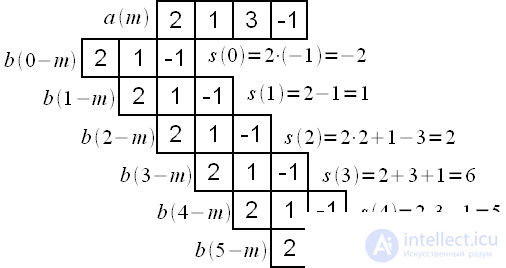
 when calculating the convolution is reflected from left to right, because
when calculating the convolution is reflected from left to right, because 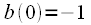 the very first count (the earliest in time) and it should also be processed first.
the very first count (the earliest in time) and it should also be processed first.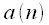 and
and 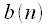 - periodic with the same period
- periodic with the same period 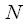 counts. Then circular convolution of the signals
counts. Then circular convolution of the signals 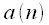 and
and 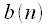 called the signal type:
called the signal type: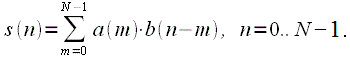
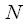 counts.
counts.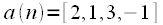 and
and 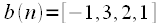 . Graphically, the calculation of cyclic convolution is presented in Figure 3.
. Graphically, the calculation of cyclic convolution is presented in Figure 3.
 . Note that due to the periodicity of the signals
. Note that due to the periodicity of the signals 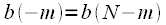 .
.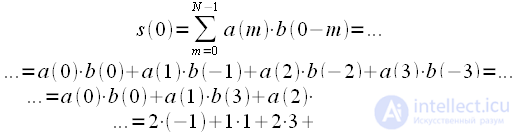
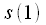 :
: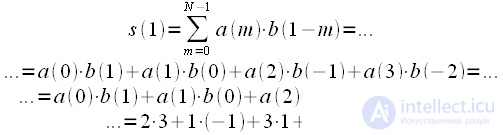
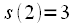 and
and 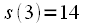 .
.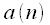 and
and 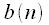 duration
duration 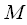 and
and 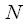 counts respectively add zeros to length
counts respectively add zeros to length 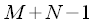 .
.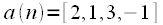 4 counts long
4 counts long 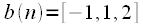 3 references long (this example was considered above).
3 references long (this example was considered above).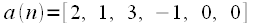 and
and 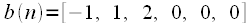 , so that in each sequence was 6 samples.
, so that in each sequence was 6 samples.
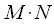 multiplications
multiplications 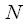 and
and 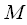 - the length of the convolved signals, and when calculating a linear convolution through a cyclic
- the length of the convolved signals, and when calculating a linear convolution through a cyclic 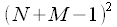 multiplications and additions. However, consider the discrete Fourier transform of cyclic convolution:
multiplications and additions. However, consider the discrete Fourier transform of cyclic convolution: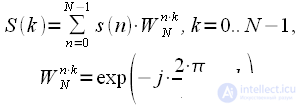
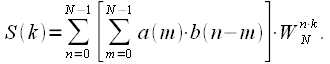
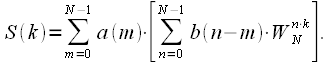
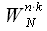 as:
as: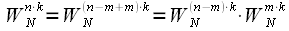
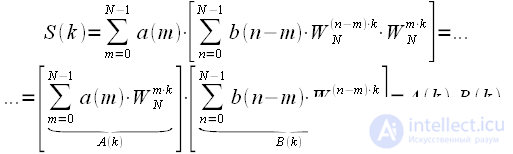

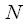 then we can propose the following method for calculating cyclic convolution. Source sequences
then we can propose the following method for calculating cyclic convolution. Source sequences 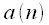 and
and 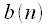 ,
, 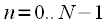 can be filled with zeros to length
can be filled with zeros to length 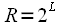 Since for effective lengths of an integer power of two, efficient FFT algorithms have been developed, then we apply the convolution calculation scheme presented in Figure 5. At the output, we obtain
Since for effective lengths of an integer power of two, efficient FFT algorithms have been developed, then we apply the convolution calculation scheme presented in Figure 5. At the output, we obtain 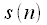 ,
, 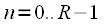 from which you need to take only the first
from which you need to take only the first 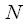 counts.
counts.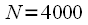 , but
, but 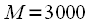 . Direct linear convolution calculation will require
. Direct linear convolution calculation will require 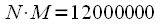 (12 million) multiplication and addition operations.
(12 million) multiplication and addition operations.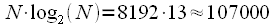 complex multiplication operations or 428000 real multiplication operations. There will be only 3 such blocks of FFT, plus you need to take into account 8192 complex multiplications of the spectra, total
complex multiplication operations or 428000 real multiplication operations. There will be only 3 such blocks of FFT, plus you need to take into account 8192 complex multiplications of the spectra, total 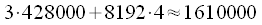 , which is almost 7.5 times lower than if we considered linear convolution in the forehead.
, which is almost 7.5 times lower than if we considered linear convolution in the forehead.
Comments
To leave a comment
Digital signal processing
Terms: Digital signal processing