5.2.4 Decision making methods

Methods for analyzing and solving problems (decision-making methods) may vary depending on the type of tasks or problems being solved. Problems can be classified as follows:

• standard problems with a clear structure, causal relationships, analogues;
• well-structured problems that can be broken down into sub-problems, blocks of questions, for each of which there is usually a set of solutions;
• semi-structured problems in which directions of the solution are not always visible, cause-and-effect relationships, problems themselves are not formulated clearly enough;
• unstructured problems, which usually have no analogues, cause-and-effect relations are not completely clear, ways of solving are not defined. A classic example is natural and man-made disasters with great social consequences.

To resolve standard and some well-structured problems, there is a set of standard, stereotypical solutions in specific situations set forth in regulatory documents: instructions, rules, standards, manuals, etc. They clearly and definitely regulate the sequence of analyzing situations and solving problems.

However, most management problems are far from stereotype. To resolve them, different methods can be applied, used at different stages and procedures of the decision-making process.

All decision-making methods can be divided into two groups: formalized (mathematical) and non-formalized (heuristic) . Formalized methods based on obtaining quantitative results of calculations are used in resolving well-structured and partially weakly structured problems to evaluate solutions, select and substantiate the optimal variant. Non-formalized methods are used in solving complex weakly structured and unstructured problems to generate solutions, analyze and evaluate them, select and justify the best solution.

Formalized methods used to justify and select optimal solutions include:

• economic-mathematical models and methods (EMM), formalizing the relationship of processes and phenomena;
• system analysis, which allows to identify the interaction of components of systems, strategy ^{* of} their development;
• expert estimates and judgments that allow qualified specialists to assess the significance of events, phenomena, factors, forecasts of the development of systems and subsystems, the ratio of deterministic and probabilistic factors.

In the aggregate, various mathematical methods, combined by the common task of justifying the best solutions, are called methods of operations research .

Methods of research operations are divided into the following four main groups: analytical, statistical, mathematical programming, game-theoretic.

Analytical methods are characterized by the fact that between the conditions of the problem being solved and its results analytical and formula dependences are established. These methods include: the theory of probability, the theory of Markov processes, the theory of mass service, the method of dynamics of means. Probability theory is the science of patterns in random phenomena. With the help of the theory of probability solutions are developed, depending on the conditions of a random nature. The theory of Markov processes is developed to describe operations that develop randomly in time. The queuing theory considers mass repetitive processes. The method of dynamics of averages is used in cases when it is possible to make dependencies between the conditions of an operation and its result, based on the average characteristics of conditions.

Statistical methods are based on the collection, processing and analysis of statistical data obtained as a result of actual actions, and artificially developed by statistical modeling. These methods include sequential analysis and statistical test method. Sequential analysis provides an opportunity to make decisions based on a number of hypotheses, each of which is immediately sequentially checked. The method of statistical tests (Monte-Carlo method) consists in the fact that the course of operations is played (simulated) on a computer with all the inherent accidents of the operation.

Mathematical programming is a series of methods designed to best distribute the limited resources available, as well as to draw up a rational plan of operation. Mathematical programming is subdivided into linear, nonlinear, and dynamic. This also usually includes network planning methods. Linear programming is used in cases where the conditions for performing an operation are described by a system of linear equations or inequalities. If the indicated dependencies are nonlinear, the nonlinear programming method is used. Dynamic programming serves to select the best plan for performing multi-step actions, when the result of each subsequent stage depends on the previous one. Network planning is designed to develop and implement a rational plan for the implementation of the operation, consisting of a large number of interrelated actions, providing for the solution of the problem in the shortest possible time and with the best results.

Game-theoretic methods are used to justify decisions in conditions of uncertainty of the situation. Game-theoretic methods include: game theory and the theory of statistical solutions. Game theory is used in cases where the uncertainty of the situation is caused by the deliberate, malicious actions of the conflicting party. The theory of statistical decisions is applied when the uncertainty of the situation is caused by objective circumstances that are either unknown or of a random nature.

Operations research focused on solving economic and industrial problems is the basis for economic and mathematical methods for modeling production processes in control systems.

Along with the quantitative results of calculations, it is necessary when taking decisions to take into account many qualitative circumstances that are not limited to unambiguous answers. Therefore, the methods of substantiating decisions based on the study of experience, intuition, and generalization of the results, including the method of expert assessments, remain important.

Non- formalized decision-making methods are developed to a lesser extent than formalized ones, and are used mainly in group decision-making. Much attention in these methods is paid to the organization of the work of the group subject of decision-making, the harmonization of the opinions of the group members when choosing the final decision. The most widely used methods used to generate a variety of alternative solutions, their analysis, evaluation and selection of the final version are the brainstorming method, the Delphi method, the scenario method, the decision tree method.

The method of brainstorming (or brainstorming) is intended to intensify the development of new ideas and solutions in difficult deadlock situations when known ways and ways to solve a problem are unsuitable. It consists in giving each member of the group the right to express various ideas on how to solve the problem, regardless of their validity and feasibility. The goal is to get as many offers as possible. All proposals are recorded without criticism and evaluation, and their discussion and analysis is made after the completion of the process of generating ideas. In the course of the discussion, the proposed ideas are analyzed in the order of their nomination and evaluated by the corresponding indicators, reflecting the existing limitations, the degree of achievement of the goals, the cost of resources, the possible efficiency. The obtained estimates of solution options are the basis for choosing the best option. The method is used to solve a variety of applied problems.

The Delphi method is one of the group peer review methods and does not require the team members to work together. Moreover, the members of the group are not allowed to meet and exchange views on the problem being solved, that is, the independence of the members of the group is ensured. The method involves the analysis and selection of solutions by performing the following multi-step cyclic procedure:

1. Group members are provided with information about the problem situation and are invited to evaluate possible solutions for a set of indicators.
2. Each member of the group anonymously and independently gives an assessment and justification of solution options or offers their own options.
3. All assessments and opinions of group members are collected in the center and summarized in a consolidated document.
4. Each team member receives a copy of the consolidated document. Acquaintance with the opinion of other participants may change his opinion on possible solutions to the problem.
5. Steps 3 and 4 are repeated as many times as necessary to achieve a consistent solution.

The Delphi method is most effective in developing solutions for complex, little-studied, unique problems, characterized by high uncertainty of the initial situation and requiring the involvement of specialists of different profiles. It requires a significant investment of time and a clear organization of the procedure for its implementation.

The scenario method , which is one of the forecasting methods, makes it possible to determine the likely trends of events and the possible consequences of the decisions made in order to select the most appropriate management alternative. The method involves the participation in the development of scenarios for the development of the analyzed situation by specialists of various profiles and often with different views on the problem under consideration. It includes techniques and methods for a meaningful and formalized description of a problem situation and specific methods and algorithms for constructing and researching scenarios for its development with extensive use of new information technologies.

A scenario is a hypothetical picture of a consistent development in time and space of events, representing in aggregate the evolution of a controlled object in the section of interest to the researcher. In the scenario, the causal dependences of the parameters that determine the possible dynamics of changes in the state of the object, the operating factors and the conditions in which these changes occur will be fixed in an explicit form. The scenario is some relative, conditional assessment of the possible development of the system, since it is always built within the framework of assumptions about future development conditions, which are often fundamentally unpredictable.

The scenario-based decision-making method provides for multi-variability, that is, the development of several alternative options for the possible development of the situation, consideration of which allows determining critical situations for decision-making, as well as determining the possible consequences of the proposed solutions to compare them and select the most effective.

There are variations of the practical implementation of the method of scenarios, differing in the content and completeness of the scenarios developed by individual specialists and the organization of the procedures for their development [3].

The decision tree method is applicable to both individual and group decision making. It is used to solve complex problems, characterized by great uncertainty and requiring an exact sequence of solutions. Each decision may have several possible outcomes, each outcome has its own probability of occurrence. Each subsequent set of possible solutions depends on the specific outcome of the previous decision. The decision tree is a schematic representation of the process of making consecutive decisions and consists of branches — decision variants and nodes — corresponding outcomes. For each outcome, the probability of its occurrence and the amount of winnings (income), which can be obtained taking into account this probability, is calculated. The costs associated with each decision are put on the appropriate branch. These expenses are deducted from expected income to determine net income. The calculations are based on data characterizing the problem situation (the problem being solved) and the conditions in which it arose.

The calculation is carried out for each decision vector from the initial decision making node to the end node of the corresponding outcome, with branch selection leading to the maximum gain and returning to the previous decision making node, which is assigned this winning value. Alternative branches (with lower winnings) are crossed out.

After successively calculating all the decision vectors, the optimal decision vector is selected, leading to the maximum net gain, provided that the events go as expected.

As an example, consider the following situation [4]. The bank decides whether to check the client’s competitiveness with the help of an audit firm before issuing a loan in the amount of $ 15,000. An audit firm takes $ 80 from the bank for each check. Thus, the bank faces two problems: the first is whether to conduct a check or not, the second is to issue a loan after that or not. As a result of the analysis of statistical data, the probabilities of possible outcomes are calculated, taking into account the recommendation of the audit firm (to issue or not issue a loan) and the return or non-return by the client of the loan.

The decision tree of this problem is shown in fig. 4.5.

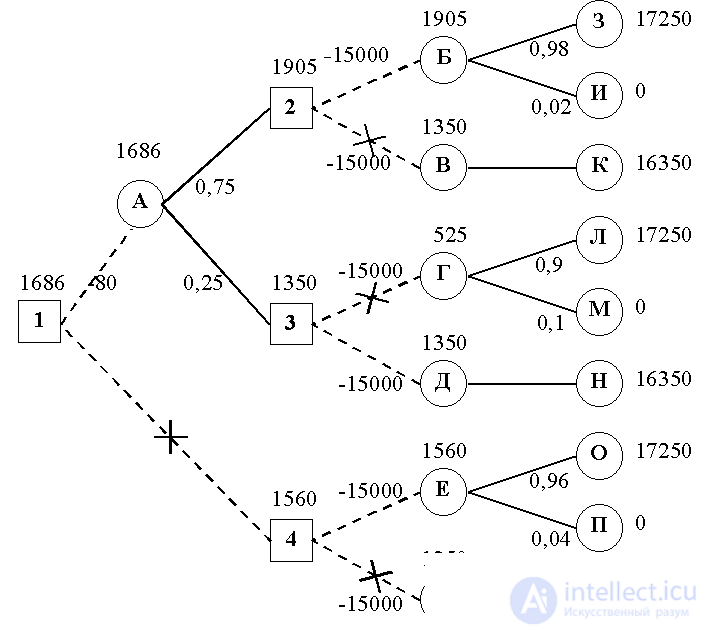
Fig. 4.5. Decision tree

In the diagram, the dashed lines correspond to the decisions made, the solid lines to the possible outcomes. Square nodes denote decision points, round nodes denote the appearance of outcomes.

The branches of the scheme have the following contents: 1-A - conducting an audit; 1-4 - the absence of an audit; А-2 - recommended loan; А-3 - loan disbursement is not recommended; 2-B, 3-G, 4-E - a loan is issued; 2-B, 3-D, 4-F - no loan is issued; Б-З, ГЛ, Е-О - money returned at 15% per annum; BI, GM, EP — money not returned; В-К, Д-Н, Ж-Р - money is invested at 9% per annum. Calculations for simplicity are not given. The rightmost column indicates the amounts that can be received at the end of the year.

The diagram shows the arrows the sequence of decisions leading to the maximum net income: In square 1, we use the audit. If the loan is recommended by the firm, then in square 2 - to issue a loan, if not recommended, then in square 3 - not to issue a loan, but to invest this money at a stable 9% per annum.

As already indicated (. 4.2.2), a decision can be made alone (an individual decision) or collectively (a group decision). An individual decision is made by choosing an alternative in accordance with the individual preferences of the decision maker. Group selection involves making a decision ^* based on the agreement of individual preferences of group members. This matching is based on the group selection principle , which defines the matching rule and the choice of the preferred solution. Consider the most common principles of group choice.

The principle of the dictator . In accordance with this principle, the preference of one person of a group is taken as a group preference. Due to the fact that this principle does not take into account the preferences of other members of the group, the concept of group decision making loses its meaningful meaning. Essentially, group preference in this case corresponds to individual preference (a joke is known: "We consulted here, and I decided"). The dictator principle is characteristic of military organizations and is widely used when making decisions in emergency situations.

The principle of the majority of votes . In accordance with this principle, a decision is recognized as preferable, for which the number of members of the group (votes), exceeding a certain threshold (C), was expressed. Depending on the value of this threshold, there are variations of the principle under consideration. With C = 1/2 (plus one vote) they talk about the principle of simple majority of votes, with C = 2/3 - about the principle of a majority of 2/3 votes (or a qualified majority ), C = 1 corresponds to the absolute majority of votes .

The adoption of a group decision requires the appropriate organization of the group’s work and decision-making procedures. Rational organization of decision-making procedures, i.e. technology of the group, requires consideration of the behavior of group members and the influence of various factors on this behavior (the nature of the problem being solved, the sequence of expressing opinions, the principles of coordinating individual preferences, the emotional state of participants, etc.) The behavior of the members of the decision-making group is a complex, little-studied problem. Currently, no significant results have been achieved that allow the construction of theoretical models that adequately reflect this behavior.In the practice of group choice, there are several provisions for streamlining selection procedures. For example, on military councils, the junior in the position and title are the first to express their opinion, which ensures that the influence of the authority of senior commanders is excluded.