INTRODUCTION TO THE THEORY OF DECISION MAKING

1.1 The subject of decision theory, basic terms and definitions

Decision making theory (TPD) is a set of mathematical disciplines in which only well-described and formalized models of decision making are investigated under certain initial conditions, restrictions on choice, and choices.

Thus, the subject of TPD is the study of decision-making processes and ways to formalize them.

By decision making, we mean human activity aimed at choosing the best course of action in a particular situation [1].

Let there be some system . It distinguishes the controlled subsystem (control object) and the control subsystem . The system itself is in a certain environment (Fig. 1.1).

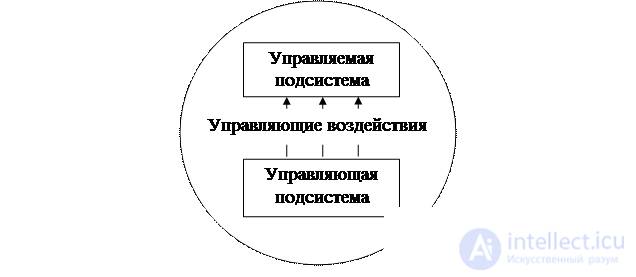
Fig. 1.1. Decision making as a management process

The controlling subsystem can influence the control object with the help of one or another control action, as a result of which the control object enters a new state.

Possible control actions are called alternatives or solutions .

The purpose of the control action is to transfer the control object to the state that is most preferable for the control subsystem. The new state of the object is determined by two factors: the selected control action and the state of the environment.

It is important that the control subsystem can not affect the environment and may not even have information about the state of the environment.

The choice of a specific controlling action (otherwise, alternative or decision) by the control subsystem is called decision making .

The purpose of making a decision is to find the optimal solution , that is, a solution that is preferable to one another or another.

A participant in the decision-making process is called a decision maker (DM).

One or several decision makers may take part in the decision making process.

So, to describe a situation in which a decision is made, you need to specify three sets:

A - many alternatives or control actions

B is the set of states of the environment,

C is the set of possible outcomes.

The term " outcomes " refers to the state in which the controlled subsystem can go.

Since the state of the controlled subsystem is determined by the choice of the controlling action and the state of the environment, each pair ( a , b ), where 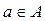, 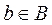matches a certain outcome 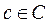. This means that there is a function 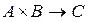. We call it the realization function and denote F.

In addition, to make a decision, each outcome must be assessed from the point of view of the decision maker, that is, to formulate another evaluation system . To measure outcomes can be used:

outcome preference ratio;

generalized criteria (for example, utility functions, efficiency functions, values);

partitioning the set of outcomes of C into classes (for example, the class of “bad” and “good” outcomes), etc.

It is important that the assessment of outcomes is subjective , as it is produced from the point of view of the decision maker.

Thus, the construction of a mathematical model of a decision-making problem is reduced to defining the sets A, B , C , the implementation function F and the evaluation system (as a utility function, preference relations, etc.) [2, p. 11-14].

1.2 Types of decision making tasks

Traditionally, the following types of decision-making tasks are distinguished:

streamlining alternatives;

the classification of alternatives or the division of alternatives into classes;

highlighting the best alternative.

For example, family members order future purchases according to the degree of necessity.

When buying a car, a person breaks all the options into two classes - cars that are suitable for the price, and cars whose value exceeds the threshold value. This is an example of a classification task.

The tasks of the third type are very often found in practice. After all the cars that are suitable for the price are known, the person chooses the best car - the one that he will eventually buy.

In addition, decision making can occur in two types of situations. In the first case , an analysis of specified alternatives is carried out, the set of alternatives is closed. In the second case, a decision rule is constructed , allowing to evaluate any alternatives .

For example, you want to determine the best pool of the city. The process involves a group of specialists, each of whom builds a ranking of the pools. Then, on the basis of individual rankings, aggregated ranking is constructed and thus the best pool is identified. In this case, an analysis of the specified alternatives - the city's basins.

An example of the second type of situation is making decisions about granting a loan in a bank. The decisive rule must be worked out before customers begin to apply to the bank. When a client contacts the bank, each time the assessment should be made according to the decision rule.

1.3 Decision making steps

Let us dwell on the most important stages of decision making, namely:

1. statement of the problem

2. defining the goal and choosing the appropriate optimality criterion,

3. the formation of conditions

4. the formation of alternatives, their preliminary analysis,

5. analysis and selection of a method for solving the problem and development of a solution algorithm,

6. evaluation of alternatives and determination of optimal (s),

7. decision making and evaluation of results.

1.4 Classification of decision-making tasks

In the scientific literature, several classifications of decision-making problems (DMS) based on various systems of attributes have been proposed [3].

The most common and essential features of the classification found in most works are:

1. the type of relationship between multiple alternatives and multiple outcomes;

2. the number of criteria;

3. the number of persons involved in the decision;

4. according to the type of model;

5. the dependence of the efficiency index (optimality criterion) and limiting factors on time;

6. using the experiment to obtain information.

1.4.1 Type of relationship between multiple alternatives and multiple outcomes. In any CRA, there are two sets of elements - a set of alternatives and a set of outcomes. On this basis, the CRA are divided into three groups.

CRA in conditions of certainty - there is a single relationship between the many alternatives and outcomes.

Example. The task of building a rating of computer shops in the city.

DSS under conditions of probable certainty or under conditions of risk — each alternative is matched with a set of outcomes with some probabilities of their implementation, these probabilities are known to decision makers.

Example. Let the workshop have n machines, and the repair of the failed machine is done individually, and if the machines do not fail, then at T intervals of time a preventive repair of all machines is performed. The task is to determine the optimal value of the number of intervals T , at which the total repair costs will be minimal. Obviously, the problem can be solved if the probability p _{t of} failure of one machine at time t is known. This uncertainty represents in this case the element of "risk".

CRA under uncertainty - information about the links between the set of alternatives and the set of outcomes is missing or incomplete.

Example. Playing poker, chess.

1.4.2. Number of criteria . By the number of criteria, single-criterion (scalar) DSS and multi-criteria (vector) DSS are distinguished.

Decision making is guided by the goals to be achieved. Goals are assigned a criterion or a set of criteria with which you can assess the degree to which this goal is achieved.

Examples As an example of single-criterion CRA, we consider the problem of the optimal size of the purchased batch of goods [2, p. 20-21].

The company buys some goods during the planning period in batches of the same size. Purchased goods are used at a constant rate. As soon as the stock of goods ends, the next batch is purchased, etc. The company stores unspent goods in the warehouse for a certain fee.

The following quantities are known:

the required amount of goods for the planning period,

unit cost,

order cost of one lot (it is considered that the cost of the order does not depend on the size of the ordered lot),

the cost of storage of a unit of goods during the planning period (it is believed that the cost of storage of goods is proportional to its quantity and storage time)

It is required to determine the size of the purchased batch of goods at which the cost of the company will be minimal.

As an example of multi-criteria CRA, one can cite the task of choosing a candidate for a position. The criteria for evaluating candidates are education, work experience, age, etc.

1.4.3. The number of persons involved in the decision. Individual and group decisions are also distinguished depending on the number of experts or decision-makers.

If two people are involved in the decision-making process and their interests are opposite, then the antagonistic game theory deals with the decision-making in such a situation.

An example of a group decision-making method is rating voting in the Duma. For example, 5 people claim to be the speaker. Then each of the deputies gives his (possibly weak) ranking of these five candidates. This raises the problem of building a generalized or compromise ranking, on the basis of which it will be determined who will become the speaker.

During group expertise, situations of the following types often arise: experts have different opinions about the set of criteria, experts have different opinions about the comparative significance of criteria, experts give different evaluations of alternatives by criteria. It can be said that group selection methods make it possible to structure many alternatives in a situation of “discrepancy” of expert judgments [4].

1.4.4. According to the type of model (decision rule) .

The decision rule is called subjective if, based on the same initial information, different researchers come to different conclusions.

The following options are possible:

1. Model is objective, the decisive rule is objective.

2. The model is objective, the decisive rule is subjective.

3. The model is subjective, the decisive rule is objective.

4. The model is subjective, the decisive rule is subjective.

The construction of models is considered in the framework of operations research as a means of reflecting an objectively existing reality. When a model that correctly reflects reality is found, an optimality criterion is established, the optimal solution can be obtained in the only possible way. Based on the same data, various analysts should get the same results [1].

1.4.5. The dependence of the optimality criterion and limiting factors on time . On this basis, the CRA is divided into two large classes: static and dynamic .

The task is called static if the decision is made in the forward known and not changing information state, or in the static CRA, the performance indicator and limiting conditions do not depend on time.

If the information state in the course of the decision replacing each other, then the task is called dynamic.

1.4.6. Using experiment to get information . On the basis of the use of the experiment to obtain information, the CRA is classified into two groups: the CRA by a priori data and the CRA by a posteriori data .

Making decisions on a priori data is characteristic of the conditions of certainty and in part for the conditions of probable certainty. In conditions of uncertainty, a priori information is very small, so it is necessary to obtain new information through experiments. Experimental results provide a posteriori information.

1.5 The relationship between classes of CRA and areas of TPD

In fig. 1.2 shows the relationship between the classes of decision-making tasks and areas of TPD.

Next will be considered in detail multi-criteria CRA under certainty and risk. In the face of uncertainty, we will focus on single-criterion CRA and multi-criteria CRA, we will also consider group or collective CRA.

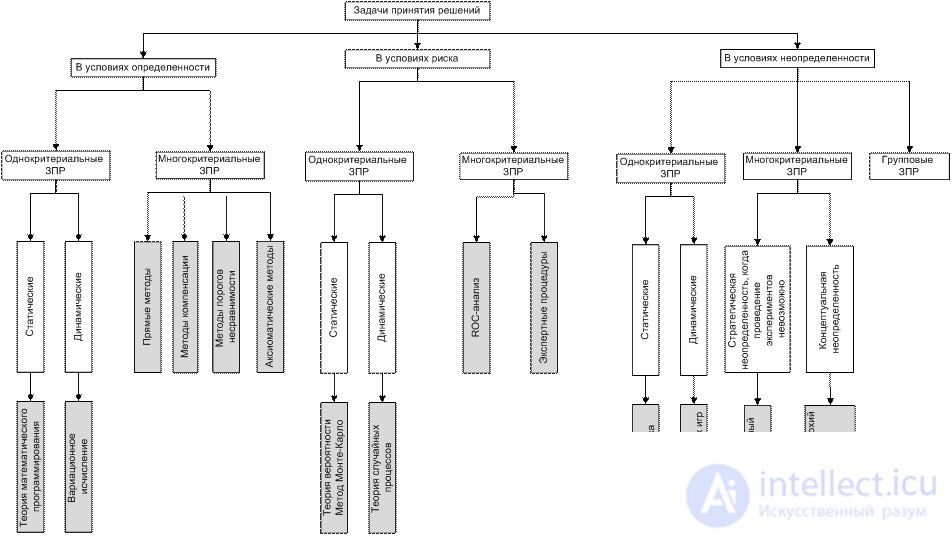
Fig. 1.2. ZPR classification