Lecture
Modern communication systems use complex signals (that is, having complex mathematical models that describe the behavior of signals) and complex methods for their processing. At the same time, combinations of elementary signals are often used to describe signals of any complexity, the models of which are described by simple mathematical expressions.
So, for the solution of a large number of radio engineering problems, the inclusion function (the Heaviside function) is widely used (Fig. 4.1.).
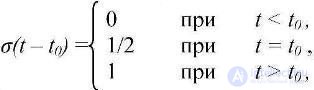 (4.1)
(4.1)
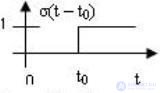
Fig. 4.1 power function
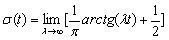 (4.2)
(4.2)
Fig. 4.2 Dynamic signal representation
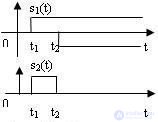
Fig. 4.3 Forming a rectangular pulse
A variant of a rectangular pulse is the so-called delta pulse, which is obtained at the limiting transition from a rectangular pulse, which with decreasing pulse duration equal to τ = (t2 - t1), simultaneously increases the amplitude E while maintaining the "area" of the pulse defined as S = τE (fig.4.4)
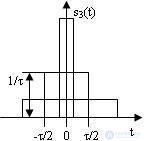
Fig. 4.4 Transition to Delta Functions
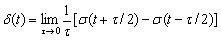 (4.3)
(4.3)
The delta function δ (t) can be interpreted as the result of differentiation of the inclusion function σ (t). The role of the delta functions in the analysis of radio circuits and signals is also large, despite the fact that the delta function is a mathematical abstraction. In particular, to determine the impulse characteristics of radio devices, pulsed signals are used, the duration of which is much less than the duration of the response of the circuit to this effect.
Significant place in the series of radio signals takes periodic signals (Figure 4.5), mathematical models of which can be represented by the expression
s (t) = s (t + kT), (4.4)
where k is any integer, and T is the signal period (the minimum time interval between repeated signal values).
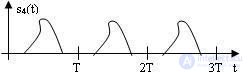
Fig. 4.5 Periodic signal
Due to their regularity, periodic signals are a good basis for the formation of various clocking and synchronizing sequences, and can also be used as carrier rings for various types of modulation.
One of the most famous periodic signals is the harmonic function.
s (t) = A cos (2πft + φ) = A cos (2πt / T + φ) = A cos (ωt + φ) , (4.5)
where A is the amplitude of the harmonic lines ***; f is the cyclic frequency of harmonic cololes *** (the reciprocal of the period of colo *** ***), f = 1 / T; ω = 2πf is the circular frequency of harmonic cola *** s; φ is the initial phase shift of the harmonic oscillation ***.
Hereinafter, the values of the signals at the current time (the instantaneous value of the signals, for example, s (t)) will be denoted by lowercase letters, to denote the amplitude of col *** ***, we will use capital letters.
The behavior of the harmonic collation in the time domain is shown in Figure 4.6. In the analysis of radio devices, in addition to the temporal representation, the representation of signals in the frequency domain is also used.
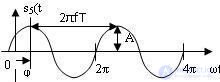
Fig. 4.6 Harmonic signal
The widespread use of the harmonic signal is due to the universality of the form of the harmonic colony ***. This versatility lies in the fact that the harmonic column does not change its shape when passing through linear chains (recall that in a linear chain the coefficients of the differential equation describing the operation of this chain are constant and do not depend on the size of the input signal). With the passage of a harmonic signal through a linear circuit, the shape (repeating the sinusoidal dependence) and the frequency of these lines *** remain unchanged, only the amplitude and the initial phase can change.
Comments
To leave a comment
Devices for the reception and processing of radio signals, Transmission, reception and processing of signals
Terms: Devices for the reception and processing of radio signals, Transmission, reception and processing of signals