The condition of self-excitation is equality
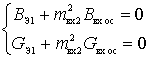 ,
,
the first of which is the phase balance condition, and the second the amplitude balance condition.
The amplifier will not be self-excited if the conductance of the circuit at its input, taking into account the feedback, will be positive:
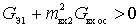 .
.
But the absence of self-excitation does not mean the invariance of the amplifier.
We introduce the stability coefficient
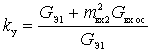 .
.
If a 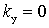 , the amplifier can be self-excited. With
, the amplifier can be self-excited. With 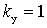 no feedback, which corresponds to the maximum stability of the amplifier. Usually take
no feedback, which corresponds to the maximum stability of the amplifier. Usually take 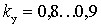 . In this case, the change of the gain and bandwidth under the action of the OS does not exceed 10 ... 20%. the closer
. In this case, the change of the gain and bandwidth under the action of the OS does not exceed 10 ... 20%. the closer 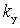 to one, the more stable the amplifier.
to one, the more stable the amplifier.
Similar reasoning is true for a negative OS: the properties of the amplifier should not undergo significant changes, so choose 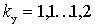 .
.
Let us find the stability condition of the amplifier with a given stability margin. When considering the previous question, we received
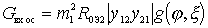 .
.
Where 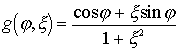 - the function that determines the dependence
- the function that determines the dependence 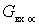 from disorder
from disorder 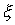 and argument
and argument 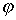 .
.
The nature of this dependence, and consequently, the active component of the input dynamic conductivity from 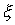 shown in the figure (solid line). As a function of the argument
shown in the figure (solid line). As a function of the argument 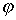 , it will change (dashed lines), approaching
, it will change (dashed lines), approaching 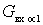 or
or  . At pic
. At pic 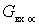 negative, with OOS - positive.
negative, with OOS - positive.
Figure 10.7.
Substitute the expression for 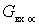 in the expression for
in the expression for 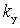
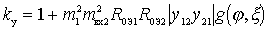 .
.
At the last lesson, we obtained an expression for the resonant gain
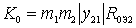 ;
;
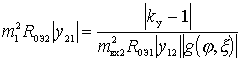 .
.
In this expression entered the signs of the absolute value 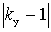 and
and 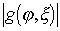 to combine both cases of OS in one formula, since with pic
to combine both cases of OS in one formula, since with pic 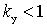 and
and 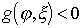 , and at OOS
, and at OOS 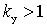 ,
, 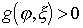 .
.
Multiplying both sides of the resulting equality by 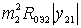 get
get
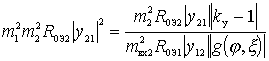 .
.
Solving this equation for 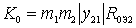 get
get
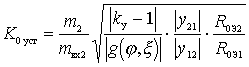 .
.
Sustainability is ensured if
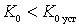 .
.
With identical circuits at the input and output of the amplifier 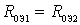 ;
; 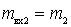 and the expression for
and the expression for 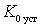 take the form
take the form
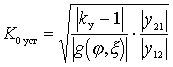 .
.
This expression shows that to obtain a large, stable gain, an amplifying device must be chosen with the maximum value of the ratio  . This relationship simultaneously characterizes the amplification capabilities of an electronic device and spurious feedback. Gain is possible if
. This relationship simultaneously characterizes the amplification capabilities of an electronic device and spurious feedback. Gain is possible if 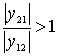 . Expression Study
. Expression Study  by
by 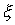 shows that it has extreme points:
shows that it has extreme points:
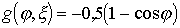 ;
;
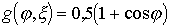 .
.
When studying the effect of the internal OS on the performance of the amplifier, it is necessary to proceed from the largest absolute value of the active component of the input dynamic conductivity.
Then
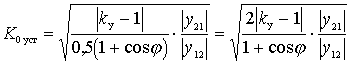 .
.
In a multi-stage amplifier, the output circuit of this stage is the input of the next stage. In the presence of an OS, it is shunted by the input dynamic conductivity of the next cascade. Because of this, its equivalent conductivity changes, which entails a change in the input dynamic conductivity and parameters of the input circuit of this cascade to an even greater degree. Thus, a multi-stage amplifier is less stable than a single-stage amplifier. However, if in each cascade the condition
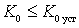 ,
,
then the decrease in stability is insignificant.


Comments
To leave a comment
Devices for the reception and processing of radio signals, Transmission, reception and processing of signals
Terms: Devices for the reception and processing of radio signals, Transmission, reception and processing of signals