5.4 Phase Modulation

During phase modulation, the amplitude of the carrier collar *** of U _{0 is} kept constant, and the phase of the carrier collar *** of φ (t) is associated with the modulating voltage e (t)

ψ (t) = ω ₀ t + k _FM e (t) + φ ₀ , (5.12)

where k _FM is the proportionality coefficient, which determines the relationship between the modulating voltage e (t) and the additional increment of the total phase of the resulting phase-modulated colo ***.
With phase modulation according to the harmonic law

e (t) = E cos (´Ωt + Θ)

the full phase of the phase-modulated col ration takes the value

ψ (t) = ω ₀ t + k _FM E cos (Ωt +) + φ ₀ (5.13)

The maximum additional deviation of the phase of the carrying colum *** with respect to the regular value of ω ₀ t is characterized by the phase modulation index M _FM :

M _FM = k _FM E. (5.14)

Thus, a complete description of the phase-modulated *** dialing modulated by the tone signal has the form:

u _FM (t) = U ₀ cos [ω ₀ t + k _FM E cos (´Ωt + Θ) + φ ₀ ] . (5.15)

Timing diagrams of the modulating and carrier signals, as well as the phase-modulated colo *** are shown in Figure 5.5.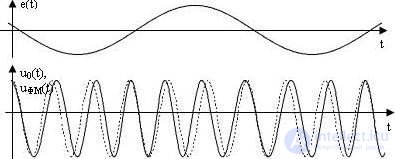

Fig. 5.5 Phase Modulation:
a) modulating signal; b) carrier ring *** (dashed line) and phase-modulated ring *** (solid line)

Determining the spectrum of a phase-modulated signal, even in the case of simple modulating signals, is a rather complicated task. The exception is the case with a small phase modulation index (M _FM << 1). In this case, at zero initial phase shifts (Θ = 0 and φ ₀ = 0), the voltage (4.15) can be represented as:

u _FM (t) = U ₀ cos [ω ₀ t + M _FM cos´Ωt].
u _FM (t) = U ₀ cos (ω ₀ t) х cos (M _ФМ cos´Ωt) - U ₀ sin (ω ₀ t) sin (M _ФМ cos´Ωt) . (5.16)

Due to the smallness of the argument (M _FM cos´Ωt << 1) of the trigonometric functions cos (M _FM cos´Ωt) and sin (M _FM cos´Ωt), the approximate relations cos (M _FM cos´Ωt) ~ 1 and sin (M _FM cos´Ωt) ~ M _FM cos´Ωt. Taking into account these approximations, expression (5.16) is reduced to the form:

u _FM (t) = U ₀ cos (ω ₀ t) - (U ₀ M _FM / 2) cos (ω ₀ - Ω) t + (U ₀ M _FM / 2) cos (ω ₀ - Ω) t . (5.17)

In terms of its form, expression (5.17) for phase-modulated wheels *** with M _FM << 1 resembles the expression for amplitude-modulated wheels *** *** (5.5): carrier ring *** with frequency ω ₀ and amplitude U ₀ and two side components with the same amplitudes equal to U ₀ M _A / 2 and frequencies equal to (ω ₀ - ´Ω) and (ω ₀ + ´Ω). The difference in the composition of the spectra of amplitude-modulated and phase-modulated col ues *** lies only in the fact that in these col ods, the components with a frequency equal to (ω ₀ - ´Ω) have opposite signs. The frequency band occupied by the phase-modulated signal in this case is also equal to

P _FM ~ 2 ´Ω . (5.18)

For large phase modulation indices (M _FM << 1), the dependence between the frequency bands occupied by the modulating and phase-modulated signals obeys more complex expressions than, for example, the relation (5.18).