Lecture
Please note that this section deals with the notion of a degree only with a natural indicator and zero.
The concept and properties of degrees with rational exponents (with negative and fractional) will be discussed in the lessons for grade 8.
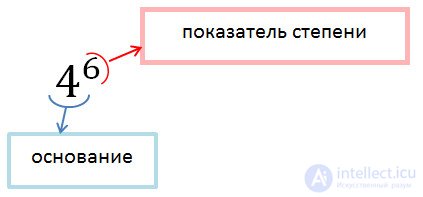
So, let's understand what is the power of the number. To write the product of the number itself on itself several times use the abbreviated notation. Thus, instead of the product of six identical factors 4 • 4 • 4 • 4 • 4 • 4, they write 4 6 and say “four to the sixth degree”.
4 • 4 • 4 • 4 • 4 • 4 = 4 6The expression 4 6 is called the power of the number, where:
In general, the degree with the base "a" and the index "n" is written using the expression:
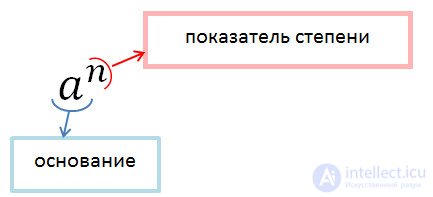
The degree of the number "a" with a natural index "n", greater than 1, is the product of "n" equal factors, each of which is equal to the number "a".

The record a n reads like this: “but to the power of n” or “the nth power of the number a”.
The exceptions are records:
Of course, the expressions above can be read to determine the degree:
Special cases occur when the exponent is one or zero (n = 1; n = 0).
The degree of the number "a" with the index n = 1 is the number itself:
a 1 = a
Any number in the zero degree is one.
a 0 = 1
Zero in any natural degree is zero.
0 n = 0
The unit to any degree is equal to 1.
1 n = 1
The expression 0 0 ( zero to zero power ) is considered to be meaningless.
When solving examples, one must remember that exponentiation is called finding the value of a degree.
Example. Raise to degree.
| 3 |
| four |
| 3 |
| four |
| 3 |
| four |
| 3 |
| four |
| 3 |
| four |
| 3 • 3 • 3 • 3 |
| 4 • 4 • 4 • 4 |
| 81 |
| 256 |
The basis of a degree (a number that is raised to a power) can be any number — positive, negative, or zero.
When raising to a power of a positive number, a positive number is obtained.
When constructing a zero natural degree, a zero is obtained.
When raising a negative number to a power, the result can be both a positive number and a negative number. It depends on whether the exponent is odd or odd.
Consider examples of raising to the power of negative numbers.

From the considered examples it is clear that if a negative number is raised to an odd power, then a negative number is obtained. Since the product of an odd number of negative factors is negative.
If a negative number is raised to an even power, then a positive number is obtained. Since the product of an even number of negative factors is positive.
A negative number raised to an even power is a positive number.
A negative number raised to an odd degree is a negative number.
The square of any number is a positive number or zero, that is:
a 2 ≥ 0 for any a.
When solving examples of exponentiation, they often make mistakes, forgetting that the entries (- 5) 4 and -5 4 are different expressions. The results of the exponentiation of these expressions will be different.
Calculate (- 5) 4 means to find the value of the fourth power of a negative number.
(- 5) 4 = (- 5) • (- 5) • (- 5) • (- 5) = 625While finding -5 4 means that the example needs to be solved in 2 steps:
Example. Calculate: - 6 2 - (- 1) 4
- 6 2 - (- 1) 4 = - 37The calculation of the value is called exponentiation action. This is the action of the third step.
In expressions with powers that do not contain parentheses, they first execute a power , then multiply and divide, and at the end add and subtract.
If there are brackets in the expression, then first in the order specified above, perform actions in brackets, and then the remaining actions in the same order from left to right.
Example. Calculate:
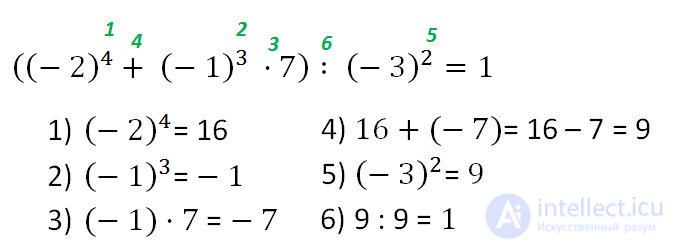
Comments
To leave a comment
Arithmetic
Terms: Arithmetic