Lecture
If you know how much a part is from a whole, then by a known part you can “restore” the whole.
To do this, we use the rule for finding an integer (number) by its fraction (part).
To find a number by its part , expressed by a fraction, it is necessary to divide this number into a fraction.
Example. Consider the task.
The train traveled 240 km, which amounted to 15/23 all the way. Which way should the train go?
Decision. 240 km is part of the whole journey. The same kilometers are expressed by fraction 15/23 from the entire path. The denominator of the fraction says that the whole path is divided into 23 parts, and 15 such parts make up 240 km (the numerator of the fraction is 15).
So you can find how much is 1/23 of the way.
240: 15 = 16 (km).The entire path (integer) is always denoted by one, which can be expressed in fractions 23/23.
So, to find the whole path (23 parts, each of which is 16 km), you need:
16 • 23 = 368 (km)A brief record of the solution of such a problem can be made as follows.
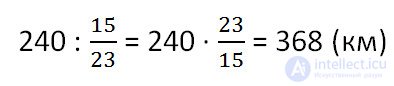
Answer: the train must pass 368 km.
Often, tasks of this type are more complicated than the considered task above, and more complex tasks have to be solved in several actions.
Consider the task.
In preparation for the dictation of the English language, Olya learned a quarter of all the words given by the teacher. If she had learned 4 more words, then a third of all words would have been learned. How many words did Ole have to learn?
Decision. As usual, we emphasize in the statement of the problem all the important data.
As can be seen from the condition, the four unlearned words are a part of all words, which can be found in the form of a fraction difference.
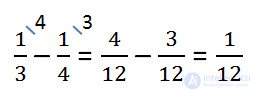
Such a part of all words is 4 words.
So, 4 words is 1/12 of all words (the whole). Now, by the rule of finding a number by its part , we divide the given numerical value by the corresponding fraction (1/12).
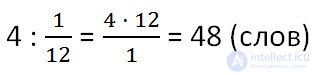
Answer: only 48 words needed to be learned to dictation.
Comments
To leave a comment
Arithmetic
Terms: Arithmetic