Rounding numbers

Numbers are rounded when full accuracy is not needed or impossible.

Natural numbers are rounded to tens, hundreds, thousands, etc. The names of the digits in the digits of the natural number can be recalled to the subject numbers.

Depending on the category to which the number should be rounded, we replace the digit in the digits of units, tens, etc. with zeros.

If the number is rounded to tens, then we replace the number in the unit one with zeros.

If the number is rounded to hundreds, then the digit zero should stand in the unit discharge, and in the tens digit.

Record the result of rounding after the special sign "≈". This sign reads approximately equal.

When rounding a natural number to any digit, one should use the rounding rules .

1. Underline the digit of the digit to which the number should be rounded.
2. Separate all digits from the right of this digit with a vertical bar.
3. • If the digit 0, 1, 2, 3 or 4 is to the right of the underlined digit, then all digits that are separated to the right are replaced with zeros. The digit of the discharge, to which it is rounded, is left unchanged.
   • If the digit 5, 6, 7, 8 or 9 is to the right of the underlined digit, then all digits that are separated to the right are replaced with zeros, and 1 is added to the digit to which it was rounded.

Let us explain by example. Round off 57 861 to thousands. Perform the first two points of the rounding rules.

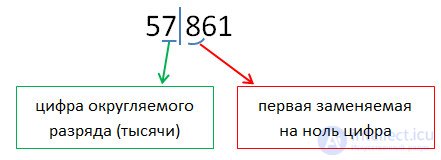
After the underlined digit there is a digit 8, which means we add 1 to the digit of thousands (we have 7), and replace all digits separated by a vertical bar with zeros.

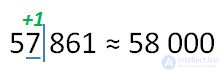
Now round 756 485 to hundreds.

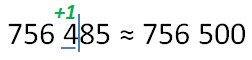
Round up 364 to dozens.

36 | 4 ≈ 360 - in the discharge of units costs 4, therefore we leave 6 in the discharge of tens without changes.

On the number axis, the number 364 is between two “round” numbers 360 and 370. These two numbers are called approximate values ​​of the number 364 with an accuracy of tens.

The number 360 is an approximate value with a flaw , and the number 370 is an approximate value with an excess .

In our case, rounding up 364 to dozens, we got, 360 - an approximate value with a disadvantage.

Rounded results are often written without zeros, adding the abbreviations "thousand" (thousand), "million" (million) and "billion" (billion).

Examples:

• 8,659,000 = 8,659 thousand
• 3,000,000 = 3 million

Rounding is also used to approximate checking the answer in calculations.

Suppose we need to count:

794 • 52 =

Before an exact calculation, let's make an estimate of the answer, rounding the factors up to the highest digit.

We conclude that the answer will be close to 40,000.

Similarly, you can perform estimation by rounding and dividing numbers.

продолжение следует...

Продолжение:

Часть 1 Rounding numbers